stereometria Namita: W ostrosłupie prawidłowym trójkątnym krawędź boczna jest trzy razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta zawartego między ścianami bocznymi tego ostrosłupa. Najpierw wyznaczam wysokość ściany bocznej i wychodzi mi ^√35₂a, dzięki temu wyznaczam drugą wysokość ściany bocznej (bo między nimi jest szukany kąt) wychodzi mi ^√35₆a. Potem z tw. cosinusów otrzymuję coś takiego: a²=(^√35₆a)²+(^√35₆a)²−2^√35₆a ^√35₆a cos/alpha i otrzymuję wynik cos\alpha=²⁴₇₀. W odpowiedziach jest wynik ³⁹₇₀. Co robię nie tak?

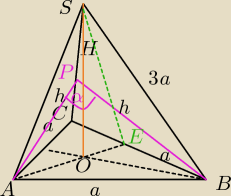
Mila: PB=PA=h− wysokość opuszczona krawędź boczną

	1
PΔBCS=		a*|SE|
	2

	1		a√35
|SE|2+(		a)2=(3a)2⇔|SE|=
	2		2

	1		a√35		1
		a*		=		*3a*h
	2		2		2

	a√35
h=
	6

	a2*35		a2*35
a2=2*		−2*		*cosα
	36		36

	17
cosα=
	35

Namita: No racje też dostaję ¹⁷₃₅. Czyli pewnie znowu mają błąd w odpowiedziach.

Mila: