
 a=10
α=450
a=10
α=450
| a√3 | 10√3 | |||
h= | = | |||
| 2 | 2 |
| 2 | 2 | 10√3 | ||||
|OB|= | h= | *5√3= | ||||
| 3 | 3 | 3 |
| 10√3 | ||
H=|OB|= | ||
| 3 |
| 1 | 5√3 | |||
SE2=OE2+H2, OE= | h= | |||
| 3 | 3 |
| 5√3 | 10√3 | |||
SE2=( | )2+( | )2 | ||
| 3 | 3 |
| 25*3 | 100*3 | 375 | ||||
SE2= | + | = | ||||
| 9 | 9 | 9 |
| √375 | 5√15 | |||
|SE|= | = | |||
| √9 | 3 |
| 1 | 5√15 | |||
Pb=3* | *15* | = oblicz | ||
| 2 | 3 |
| 1 | ||
Ppodstawy= | *10*5√3= oblicz | |
| 2 |
| 1 | ||
V= | *Ppodstawy*H | |
| 3 |


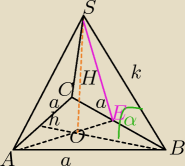
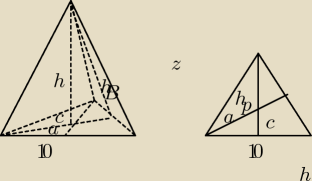 c − punkt centralny − przebicie prostej h (wysokość ostrosłupa) przez płaszczyznę podstawy
a − odległość od wierzchołka trójkąta podstawy do "c"
Ponieważ trójkąt podstawy jest trójkątem równobocznym to kąt między krawędziami wynosi 60°, a
sieczna jest połową czyli 30°, z tego wyliczamy "a" (biorąc również połowę ktawędzi)
a=5/cos30°=5/√3/2=10/√3
Nachylenie krawędzi bocznej do podstawy wynosi 45° więc:
h/a=tg45° => h=axtg45°=10/√3 x 1=10/√3
Wysokość podstawy (dla kąta 60° w wierzchołku) hp=5xtg60°=5x√3
Pole podstawy − Pp=1/2 x 10 x 5x√3=25x√3
Objętość ostrosłupa: V=Ppxh = 25x√3 x 10/√3 = 250
Żeby wyznaczyć pole powierzchni bocznej musimy obliczyć wysokość ściany bocznej hB
hB2=h2 + (hp−a)2 = (10/√3)2 + ((5x√3)−(10/√3))2 = (100/3) + (5/√3)2
hB2= (100/3) + (25/3) = 125/3
hB = 5x√5/√3
Pole pow. bocznej − PB=3x1/2x10x 5x√5/√3 = 75x√5/√3
Pole pow. całkowitej
Pc=Pp+PB=25x√3 + 75x√5/√3 = (75+75x√5)/√3
Pc=75x(1+√5)/√3
c − punkt centralny − przebicie prostej h (wysokość ostrosłupa) przez płaszczyznę podstawy
a − odległość od wierzchołka trójkąta podstawy do "c"
Ponieważ trójkąt podstawy jest trójkątem równobocznym to kąt między krawędziami wynosi 60°, a
sieczna jest połową czyli 30°, z tego wyliczamy "a" (biorąc również połowę ktawędzi)
a=5/cos30°=5/√3/2=10/√3
Nachylenie krawędzi bocznej do podstawy wynosi 45° więc:
h/a=tg45° => h=axtg45°=10/√3 x 1=10/√3
Wysokość podstawy (dla kąta 60° w wierzchołku) hp=5xtg60°=5x√3
Pole podstawy − Pp=1/2 x 10 x 5x√3=25x√3
Objętość ostrosłupa: V=Ppxh = 25x√3 x 10/√3 = 250
Żeby wyznaczyć pole powierzchni bocznej musimy obliczyć wysokość ściany bocznej hB
hB2=h2 + (hp−a)2 = (10/√3)2 + ((5x√3)−(10/√3))2 = (100/3) + (5/√3)2
hB2= (100/3) + (25/3) = 125/3
hB = 5x√5/√3
Pole pow. bocznej − PB=3x1/2x10x 5x√5/√3 = 75x√5/√3
Pole pow. całkowitej
Pc=Pp+PB=25x√3 + 75x√5/√3 = (75+75x√5)/√3
Pc=75x(1+√5)/√3