jjj Eto": Punkty będące środkami okręgów stycznych zewnętrznie do okręgu o równaniu x² + y² = 4 i jednocześnie do osi OX tworzą pewien zbiór. Wyznacz ten zbiór i narysuj go w układzie współrzędnych.

Eto": kompletnie nie wiem jak to ugrysc

Eto":

marta: O(0;0) − środek danego okręgu r=2 − długość promienia danego okręgu S(x;y) − środek okręgu stycznego zewnętrznie do danego okręgu i stycznego do osi O uklad rownan OS=√x²+y² OS =2+|y| /\ √x²+y²=2+|y| /\ |x|>2 =>x²+y²=4+4|y|+y² /\ x∊(−nieskonczonosci;−2)∪(2;nieskon.+) => |y|=1/4x²−1 /\ x∊(−nieskonczonosci;−2)∪(2;nieskon.+) => y=1/4x²−1 \/ y=1/4x²+1 /\ x∊(−nieskonczonosci;−2)∪(2;nieskon.+) wykresem wyznaczonego zbioru są części parabol dla argumentów : x∊(−nieskonczonosci;−2)∪(2;nieskon.+)

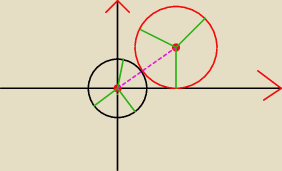
Eto": dzieki skumalem