geometria analityczna
gk18: dane są punkt A(−3;−3) i prosta k : y = 4x+2. Przez punkt A poprowadzono prostą l nachyloną do
osi OX pod kątem 135 stopni. Oblicz pole figury ograniczonej przez oś OY oraz proste k i l.
Proszę o pomoc.
Obliczyłam już równanie prostej l : y=−x−6 i narysowałam obie prostej w układzie współrzędnych.
Niestety wydaje mi się, że w poleceniu jest błąd i figura powinna być ograniczona jest przez
oś OX. Czy ktoś mógłby to przeliczyć?

1 mar 18:50
gk18: odpowiedź to P = 6,4
1 mar 18:53
gk18: mógłby ktoś pomóc?

1 mar 20:34
Saizou :
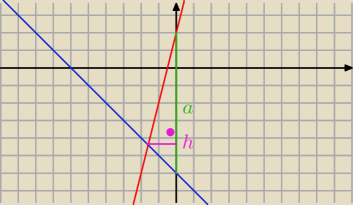
prosta nachylona do OX pod kątem 135
o i przechodząca przez punkt A ma postać y=−x−6
| | 8 | | 22 | |
punkt przecięcia prostych to P(− |
| :− |
| ) |
| | 5 | | 5 | |
| | 8 | |
zatem h= |
| , podstawa a=8 |
| | 5 | |
1 mar 20:51
dero2005:
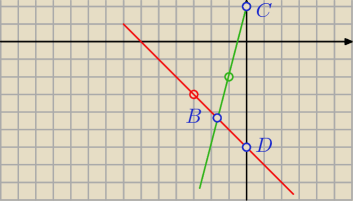
B(−
85, −
225)
C(0, 2)
D(0, −6)
|x
B, y
B, 1|
S = |x
C, y
C, 1| =
12 |x
B*y
C + x
C*y
D + x
D*y
B − x
D*y
C − x
B*y
D − x
C*y
B| =
|x
D, y
D, 1|
= 6,4
1 mar 20:54
Skipper:
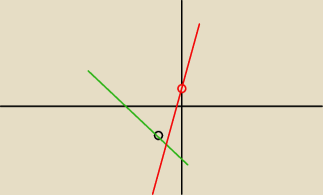
... treść jest OK−

1 mar 20:56


 prosta nachylona do OX pod kątem 135o i przechodząca przez punkt A ma postać y=−x−6
prosta nachylona do OX pod kątem 135o i przechodząca przez punkt A ma postać y=−x−6
 B(−85, −225)
C(0, 2)
D(0, −6)
|xB, yB, 1|
S = |xC, yC, 1| = 12 |xB*yC + xC*yD + xD*yB − xD*yC − xB*yD − xC*yB| =
|xD, yD, 1|
= 6,4
B(−85, −225)
C(0, 2)
D(0, −6)
|xB, yB, 1|
S = |xC, yC, 1| = 12 |xB*yC + xC*yD + xD*yB − xD*yC − xB*yD − xC*yB| =
|xD, yD, 1|
= 6,4
 ... treść jest OK−
... treść jest OK−