Dowodzenie; trójkąty EMPE: W trójkącie ABC poprowadzono środkowe AD, BE i CF i połączono punkty D, E, F. Wykaż, że środkowe trójkąta DEF zawierają się w środkowych trójkąta ABC.

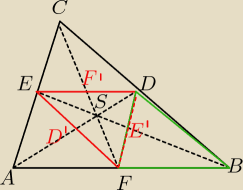
Mila: ED||AB i DF||AC i EF||BC

	1
ΔDFB∼ΔABC (w skali		)
	2

EB odcinek łączący B ze środkiem AC, Z tw. Talesa:

DB		BC		DB		DE'		1		DE'
	=		⇔		=		⇔		=
DE'		CE		BC		CE		2		CE

	1
DE'=		|CE| ⇒E' jest środkiem FD ,
	2

czyli E'E to srodkowa ΔDEF i E'E zawiera się w środkowej EB Analogicznie środkowa FF' zawiera się w środkowej FC i środkowa DD' zawiera się w środkowej AD.