Nim i maks Makaveli: Niby proste a problem.. Dla funkcji f: [−6;8} gdzie f(x)= √100−x², wyznaczyć najmniejsza i największą wartość. Ma ktoś chęć na rozwiązanie?

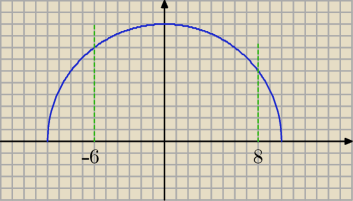
aniabb: x=0 f(0)=10 max x=−6 f(−6)=8 x=8 f(8)=6 min

Makaveli: Niesamowite, dzięki wielkie.

pigor: ...otóż, z D_f=<−10;10> i x∊<−6;8> masz f(x)=√100−x²= √100(1−0,01x²)= 10√1−(0,01x)² ⇒ ⇒ f(0)=10*1= 10 − ekstremum lokalne, a f(−6)= √64= 8 i f(8)= 6, zatem 6< 8< 10, więc f_najmn.= 6, zaś f_najw.= 10 . ...

Revolv: Genialnie, dzięki Co ciekawe, miałem właśnie takie zadanie na egzaminie i obliczenia nawet sie zgadzały, tylko zapomniałem o dziedzinie, no ale nie wystarczyło na przynajmniej 1pkt....