pytanie tn: Witam! Chętnie rozwiążę zadanie (poziom R) dotyczące planimetrii. Na myśli mam zadanie, które może sprawic trudność, owocuje czymś ciekawym pod kątem przeszłej ( teraźniejszej:( ) matury. Jak ktoś coś fajnego ma to może się podzielić

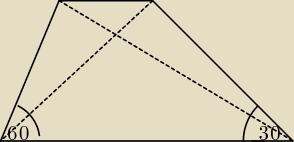
Bogdan: Już kiedyś to zadanie tu prezentowałem. Trapez: x, y − długości przekątnych x² − y² = 20, miary kątów przy dolnej podstawie: 60^o, 30^o. Obliczyć pole trapezu

Bogdan: Hej, tn co Ty na to? trudne?

Mateusz: Zadanie ode mnie: W koło o promieniu R wpisujemy trójkąty w ten sposób że środek koła należy do jednego z boków Oblicz obwód trójkąta o największym polu.

Patryk: wiem ,ze nie moje ale czy ob=2R(√2+1) ?

Mateusz: Zgadza sie, Patryk

Patryk: oho ho ho ,dzięki za odp

pigor: ..., jest to obwód 2p=2R+2R√2= 2R(1+√2), Δ−a prostokątnego, równoramiennego o stałej podstawie 2R i wysokości h=R, czyli o polu P_max.= P(h=R)= ¹₂*2R*R= R², spośród ΔΔ−ów o wysokościach h≤ R...

Mateusz: No dobra Panowie zadanie miał rozwiazac tn szczegolnie dlatego ze ostatnio przerabiał pochodne z tego co widziałem dam mu zaraz inne

Mateusz: W trójkącie ABC boki AC i BC są równe okrąg ktorego srednicą jest wysokosc CD trójkąta przecina boki trójkąta w punktach dzielących te boki w stosunku m do n licząc od wierzchołka C. Oblicz pole trojkata ABC mając daną dlugość wysokości CD=a.

tn: Wielkie dzięki. Jutro do nich wrócę i zaprezentuję rozwiązania, jeśli dam radę

Eta: Zadanie podane przez Bogdana ... wciąż czeka ...na proste rozwiązanie

Patryk: czy w zadani Bogdana x i y to zmienne czy niewiadome ?

Ajtek: Niewiadome, długości przekątnych i x>y

Patryk: no,tak się tylko pytam

Eta:

Licealista D: Nie mogę wpaść na żadną zależność zrobiłem przekątne jako dwa trójkąty prostokątne. Wiem też, że suma kątów przy tym samym ramieniu jest 180 stopni . Chciałem uzależnić dłuższą podstawę od h ale nie mogę :< ... jakaś podpowiedź mała

Kipic: Mam pytanie czy odpowiedz do tego zadania co Bogdan napisał to wychodzi pole P=5√3

Eta: P=5√3

Kipic: e no ot git teraz takie zeby dali i mozna robic

konda: Z twierdzenia cosinusów dochodzę do równania 40= −ac −cb +√3bd −√3ad Nie wiem czy to dobry trop

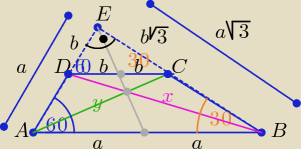
Eta: Trójkąty ABE i DCE są prostokątne o kątach 30^o, 60^o, 90^o

	a*a√3		b*b√3		√3
P(tr)=P(ΔABE)−P(ΔDCE)=		−		= (a2−b2)*
	2		2		2

x²=b²+3a² y²=a²+3b² − −−−−−−−−−−−−− x²−y²= 2(a²−b²) ⇒ a²−b²= 10

	√3
P(tr)= 10*		= 5√3
	2

Licealista D: Najciężej wpaść na pomysł rozwiązania . A to wszystko takie łatwe.

Bogdan: Ety rozwiązanie jest bardzo eleganckie, witaj Eto . Jest jeszcze inny sprytny sposób na proste rozwiązanie tego zadania

Eta: Witam Bogdanie ...może z podobieństwa? lub z długości odcinka łączącego środki podstaw ..tak?

Licealista D: Chętnie zrobię drugim sposobem na zapamiętanie, tylko jakim

Bogdan: Nie Eto , ale może niech młodzież najpierw trochę się pogimnastykuje

Eta: ok

Bogdan: Czy w szczególnym przypadku trójkąt może być trapezem?, jeśli tak, to co wtedy dzieje się z przekątnymi trapezu?

Eta: Hehe.... teraz już mam proste rozwiązanie

Licealista D: Wydaję mi się, że trapez ma 4 boki, trójkąt trzy boki . Więc w jakim przypadku może być trapezem. Ogólnie próbowałem podzielić trapez na dwa trapezy prostokątne i liczyć, że różnica kwadratów przekątny jest różnicą kwadratów podstaw. I wtedy z 2 trapezu zrobić układ równań. Ale nie mogłem dojść do jakiegoś wyniku. Liczyłem także z twierdzenia cosinusów i doszedłem do tego, że dłuższa podstawa to p{10) lub 10 , potem podstawiłbym to do różnic podstaw i wyliczył krótszą podstawę, która w obu prostokątnych i w wyjściowym trapezie jest taka sama. Ale wydaję mi się, że to łatwy sposób nie jest

Licealista D: Chyba, że patrząć z takiego myślenia średniego. Trójkąt to trapez ale jedna jego podstawa jest równa 0 ? . Hmm

Licealista D: @Bogdan

Bogdan: Ciepło, ciepło Licealista D

Mila: Zadania dla TN http://www.zadania.info/76892 Rozwiązuj, jutro będzie nowa porcja.