symetria osiowa joe: Wyznacz równanie prostej będącej obrazem prostej o równaniu y= −x+3 w symetri So, gdy: a) O(0,0); i tutaj zrobiłem w podpunkcie a) układem równań zgodnie z podpowiedzią nauczycielki {x'=−x {y'=−y −y'=−(−x')+3 y=−x−3 a teraz zaczynają się schodki z b) b) O(−1,1); c)O(3,3); d)O(−4,7) Proszę o pomoc jak wykorzystać ten punkt O przy robieniu tym sposobem z układem równań pozdrawiam

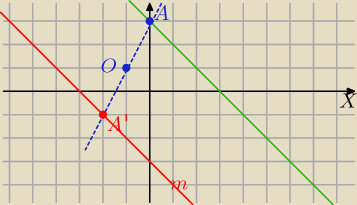
Mila: b) O=(−1,1) I sposób k: y=−x+3 Obrazem prostej w symetrii środkowej jest prosta równoległa do danej stąd m: y=−x+b A=(0,3)∊k Znajduję obraz punktu A punkt O jest środkiem AA'

	0+xA'		3+yA'
−1=		i 1=		⇔A'=(−2,−1)∊m
	2		2

−1=−(−2)+b⇔−1=2+b⇔b=−3 m: y=−x−3 I I sposób wyprowadzamy wzór na współrzędne punktu po przekształceniu przez symetrię względem punktu O(a,b) x'=−x+2a y'=−y+2b wzory łatwo wyprowadzić, skorzystać z równości OA'^→=−OA^→ a=−1 i b=1 x'=−x−2⇔x=−x'−2 y'=−y+2⇔y=−y'+2 −y'+2=−(−x'−2)+3 −y'=−2+x'+2+3 y'=−x'−3 Zamiana zmiennych y=−x−3

joe: dzięki

Mila: