Trójkąty Dude1337: 1) Oblicz najdłuższą i najkrótszą wysokość w trójkącie o bokach 6,8,12. Wiem że to nie trójkąt prostokątny, ułażyłem następujące zależności: x+y=12 x²+h²=6² y²+h²=8² Co mam dalej z tym zrobić? 2) Udownodnij że w trójkącie prostokątnym wysokość poprowadzona z wierzchołka który leży na przeciw przeciw prostokątnej(najmniejsza wysokość w tym trójkącie) wynosi h = √xy

Tad: 1) Prostokątny nie jest Policz pole ze wzoru Herona https://matematykaszkolna.pl/strona/503.html A potem wylicz poszczególne wysokości

Tad: a drugie .... to przynajmniej przepisz porządnie

pigor: ... np. tak : 2p=6+8+12= 26 obwód danego Δ, to ze wzoru Herona S_Δ=√13(13−6)(13−8)913−12)= √13*7*5, zatem ¹₂*12h₁₂= √65*7 ⇒ h₁₂= ¹₆p{65*7 − wysokość względem boku dł.12 ; ¹₂*h₆= √65*7 ⇒ h₆= ¹₃√65*7 − wysokość względem boku dł.6 przy czym h₁₂ − najdłuższa , zaś h₆ − najkrótsza szukana wysokość Δ. ...

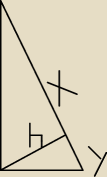
Dude1337: wykaż że h = √xy

pigor: ... zjadłem 6 w równaniu ¹₂*6h₆= √65*7. ...

Eta: pigor .... zjedz

Eta: https://matematykaszkolna.pl/forum/189247.html

pigor: ... w 2) wysokość h dzieli Δ prostokątny na 2 ΔΔ podobne tak, że ^h_x=^y_h ⇔ h²=xy ⇒ h=√xy c.n.w. . ...

Dude1337: @Eta, @ pigor @Tad DZIĘKI WIELKIE! Dzięki Wam mogę dziś iść spokojnie spać nie martwiąc się o jutrzejszą matmę. Jeszcze raz wielki dzięki.

pigor: ... o, z rozkoszą to robię, dziękuję Eta . ... :0

Janek191: z.1 Inny sposób − bez wzoru Harona a = 12 b = 8 c = 6 h₁ − wysokość do boku o długości a = 12 Mamy x² + h₁² = 6² = 36 ⇒ h₁² = 36 − x² ( 12 − x)² + h₁² = 8² = 64 zatem 144 − 24x + x² + 36 − x² = 64 24x = 116 x = 116/24 = 29/6

	29		1296		841		455
h12 = 36 − (		)2 =		−		=
	6		36		36		36

więc

	√455
h1 =		≈ 3,56
	6

−−−−−−−−−−−−−−−−−−−−−− Pole trójkąta

	√455
P = 0,5 a*h1 = 0,5*12*		= √455
	6

h₂ − wysokość do boku o długości b = 8 P = 0,5 * b *h₂ = 0,5 *8 *h₂ = 4 h₂ więc 4 h₂ = √455

	√455
h2 =		≈ 5,33
	4

−−−−−−−−−−−−−−−−−− h₃ − wysokość do boku o długości c = 6 P = 0,5 * c * h₃ = 0,5 *6*h₃ = 3 h₃ więc 3 h₃ = √455

	√455
h3 =		≈ 7,11
	3

−−−−−−−−−−−−−−−−−−− Najdłuższa wysokość to h₃ , a najkrótsza − h₁ =========================================

Janek191: Do Pigora − h₁₂ jest najkrótsza, a h₆ jest najdłuższa.

Janek191: Wzór Herona .

pigor: ..., dziękuję Janek191 i przepraszam autora tematu , no jasne, bo 6<8<12 ⇒ h₆<h₈>h₁₂ i tak miało być, ale mój translator w mojej pamięci RAM − niestety − chyba zaczyna szwankować, czas się ... leczyć