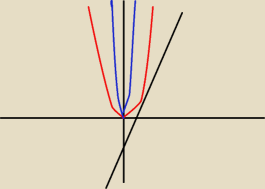
pytanie denatlu: mam taki problem, dana jest sobie prosta przypuśćmy y=2x−1 i parabola y=kx² i jak obliczyć, dla jakich k ta parabola ma punkt styczności albo przecięcie z tą prostą?

denatlu: ma ktoś jakiś pomysł?

Mateusz: Układ rownan złozony z rownania paraboli i rownania prostej musi miec jedno albo dwa rozwiązania

denatlu: tutaj z delty nie idzie

Mateusz: Jak nie idzie? Jak idzie po prostu otrzymasz zbior rozwiazan w zaleznosci od parametru k

Saizou : y=2x−1 y=kx² kx²=2x−1 kx²−2x+1=0 I funkcja kwadratowa zał k≠0 Δ≥0 4−4k≥0 −4k≥−4 k≤1 k∊(−∞:1> /{0} II f. liniowa dla k=0 −2x+1=0 −2x=−1

	1		1
x=		przecina się dla x=
	2		2

zatem ostatecznie k∊(−∞:1>

denatlu: No nie, bo dla ujemnych k parabola ma ramiona w dół czyli są dwa przecięcia, a ja pytałem o jedno.

denatlu: No nie, bo dla ujemnych k parabola ma ramiona w dół czyli są dwa przecięcia, a ja pytałem o jedno.

Saizou : no to Δ=0 −4k=−4 k=1 oraz f. linowa dla k=0 ostatecznie k∊{0:1}

denatlu: no własnie, mówiłem, że ten sposób nie działa bo mam w wyniku k ujemne, trzeba wzory vieta.

Saizou : to sprawdź np. dla k=1 y=x² y=2x−1 x²=2x−1 x²−2x+1=0 (x−1)²=0 x=1 y=1 punkt styczności to P=(1;1)

denatlu: troche źle powiedziałem od początku. Dziedzina to same x>0. Czyli już wiadomo, dla każdego k<0 będzie jedno przecięcie. Ale jeszcze dalej, moim zdaniem, dla k<1 też będą przecięcia a odpowiedź tego nie przewiduje.

Saizou : ale dziedzina funkcji liniowej czy kwadratowej ?

denatlu: obydwu. Patrz tylko na x>0, lewej strony od osi OY nie ma