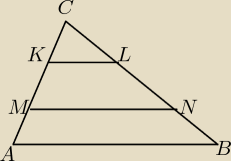Odcinki KL i MN są równoległe do podstawy AB trójkąta ABC. Stosunek pól figur KLC, MNLK i ABNM
w podanej kolejności wynosi 1:8:7 Oblicz stosunek długości odcinków |KL| : |MN| : |AB|.
| PΔKLC | x | 1 | 1 | ||||
= | =( | )2=k2=⇔ΔKLC∼ΔABC w skali | ⇔ | ||||
| PABC | 16x | 4 | 4 |
| 1 | ||
KL= | |AB|⇔|AB|=4|KL| | |
| 4 |
| PΔKLC | x | 1 | 1 | 1 | |||||
= | = | =( | )2⇔ΔKLC∼ΔMNC w skali | ⇔ | |||||
| PΔMNC | 9x | 9 | 3 | 3 |
| 1 | ||
KL= | MN⇔MN=3|KL| | |
| 3 |