Równanie trygonometryczne mrs17: Mam zadanie: Rozwiąż algebraicznie i graficznie równanie sin2x=cosx + |cosx| w zbiorze <0;2π> Rozpisałem to: sinxcosx + sinxcosx = 2cosx 2sinxcosx=2cosx/:2 sinxcosx − cosx=0 cosx (sinx − 1)=0 cosx=0 sinx=1 Więc powinno być dla cosinusa ^π₂ + kπ i dla sinusa ^π₂ +2kπ ,tak?

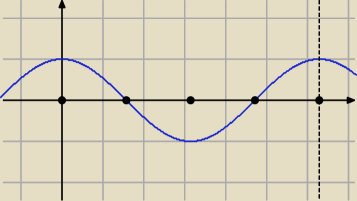
Zenon: sin2x = cosx + |cosx|

	1		3
dla x∊<0,		π>∪<		π, 2π>: sin2x = 2cosx
	2		2

	1		3
dla x∊(		,		π): sin2x = 0
	2		2

mrs17: Dziękuje,ale czy mógłbyś mi to jeszcze opisać co i jak,bo nie do końca rozumiem

Zenon: Rozważaj problem przez godzinę, a nie przez pół minuty, jeśli dalej nie będziesz rozumiał, to odpuść sobie.

mrs17: Dobra już wiem,a czy w takim zadaniu można uzasadniać swoją odpowiedź tylko rysunkiem?

Zenon: Nie

Zenon: Rysunek wspomaga rozwiązanie, jest ważnym elementem rozwiązania.

mrs17: Ok,rozumiem.

wojtek: pozwólcie, że podbiję zadanie. nie rozumiem jak narysować wykres. po prostu trzeba zaznaczyć punkty?

	π		3π
np. dla cosx<0 x∊(		;		)
	2		2

x=π więc na osi zaznaczam punkt (π,0)?

wojtek: podbijam raz jeszcze. wytłumaczy ktoś rozwiązanie graficzne?

	π		3π
jeśli wyszło x=π w tym przedziale (		;		), to patrzę jaką wartość cosx przyjmuje dla
	2		2

argumentu π i zaznaczam to jako punkt na układzie współrzędnych?

wojtek: :( ostatnie podbicie − podbicie nadziei.

krystek: Masz wytłumaczone. kreślisz funkcję sin2x i druga funkcje 2cosx tam gdzie cosx≥0 a tam gdzie cosx<0 masz zero czyli częśc osi ox

Mila: 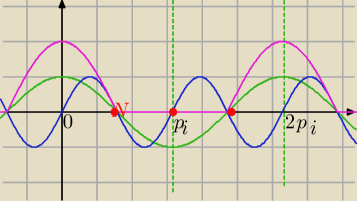y=cosx odczytuję dla jakich x ta funkcja ma wartości nieujemne

	π
cosx≥0 dla x∊<0,		>U<{3}{2}π,2π>
	2

równanie przyjmuje postać : sin(2x)=2cos(x)]]

	π
dla x∊(		,{3}{2}π) cosx<0 i równanie ma postać
	2

sin2x=0 f(x)=cos(x)+|cosx| Rozwiązania w punktach przecięcia niebieskiego o różowego wykresu napisz,

wojtek: O! Zostawiłem otwartą kartę z nadzieją, że ktoś skrobnie wykres. Opłaciło się. Dzięki Mila!

Mila:

pawel1: czy to zadanie jest poziomu z matmy podstawowej?

Osxx: Nie, to jest z rozszerzenia.