pytanie tn: Jakie figura musi spełniać warunki, aby nazwać ją deltoidem ?

krystek: Dwie pary sąsiednich boków są równe ' Przekątne połowią się pod katem prostym

Zenon: Jedna przekątna nie musi się połowić

Eta: http://pl.wikipedia.org/wiki/Deltoid

Eta: http://www.math.edu.pl/deltoid

pigor: ... myślę, że np. takie : czworokąt o przekątnych prostopadłych z których jedna jest jego osią symetrii i druga dzieli się na połowy . ...

tn: Czyżby wystarczył brak równoległości + sąsiednia równość? Wtedy stwierdzam: deltoid, a zatem mogę skorzystać z własności (np, ze wzoru na pole z przekątnych) Albo, że dzielą się przekątne pod kątem prostym. Dobrze rozumuję ?

Mila:

	e*f
Jeżeli w czworokącie przekątne e i f są prostopadłe to P=		.
	2

Dominik:

	efsinα
ogolniej − w kazdym czworokacie wypuklym pole wynosi P =		, gdzie α to kat ostry
	2

miedzy przekatnymi. dla α = 90^o sinus jest pomijany, bo wynosi 1.

tn: Czyżby wystarczył brak równoległości + sąsiednia równość? Tego nie wiedziałem! Skąd wynika ten wzór ?

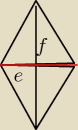
Mateusz: Na przykładzie rombu mamy sumę pol dwóch trójkątów i stąd wynika ten wzor

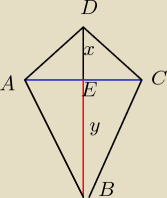
Aga1.: Deltoid IACI=e, IBDI=f x+y=f

	1		1		1		1		ef
PABCD=Ptr.ABC+PTr.ACD=		ey+		ex=		e(x+y)=		e*f=
	2		2		2		2		2

tn: Ale ja sie pytałem o wzór na pole P = e*f * 1/2 * sinα gdzie α to kat ostry pomiędzy przekątnymi e i f