Zadania AS: Moje propozycje zadań do rozwiązania − kto chce niech liczy. Przymusu nie ma. Zadanie 1. Wykaż,że funkcja x¹⁰⁰ + a*x + b ma nie więcej niż dwa miejsca zerowe. Zadanie 2. Liczb rozpoczynających się jedynką jest bardzo wiele,ale są wśród nich takie, które zwiększają się dwukrotnie,jeżeli cyfrę stojącą na końcu przenieść na początek. Spróbujcie znaleźć najmniejszą z takich liczb i podać sposób znalezienia tej liczby. Zadanie 3. Z dziewięciu cyfr 1,2,3,...,9 ułóż trzy liczby trzycyfrowe w taki sposób,by trzecia liczba była równa sumie liczby pierwszej i drugiej. Zadanie 4. 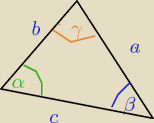Wykazać,że jeżeli dla kątów trójkąta α,β,γ zachodzi związek sinβ + sinγ sinα = −−−−−−−− cosβ + cosγ to trójkąt jest prostokątny. Zadanie 5. Wielomian x³ + 4*x² + 6*x + 4 rozłożyć na wielomian o podstawie x + 1.

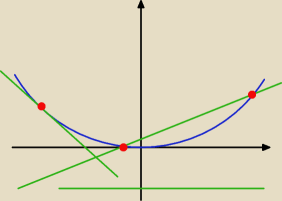
Bogdan: Dzień dobry. Nareszcie coś ciekawego. Do rozwiązania tych zadań wystarczy wiedza szkoły średniej i trochę pomyślunku. Minęło już kilka godzin od opublikowania tych zadań przez Asa i nikt ich nie ruszył, więc przedstawię ich rozwiązania w oddzielnych postach. Zad. 1. Funkcja f(x) ma miejsca zerowe ⇔ f(x) = 0. Mamy więc równanie: x¹⁰⁰ + ax + b = 0, które przekształcamy do postaci: x¹⁰⁰ = −ax − b. Po lewej stronie jest funkcja potęgowa, której wykres y = x¹⁰⁰ przypomina parabolę o wierzchołku w początku układu współrzędnych i ramionach skierowanych do góry (niebieski wykres). Prawa strona jest funkcją liniową, której wykres y = −ax − b jest linią prostą (zielony wykres). Krzywa o wykresie paraboli i linia prosta mogą mieć co najwyżej 2 punkty wspólne. Na rysunku pokazałem różne położenia prostej. Może jeszcze ktoś jednak podejmie rękawicę rzuconą przez Asa? Jeśli nie, to za jakiś czas pokażę rozwiązanie następnych zadań

tim: Zad. 3. Musi być uzasadnienie? Np. 192 + 384 = 576

tim: Zad. 5. Schematem Hornera dzielimy i zostaje: (x² + 3x + 3)(x + 1)

tim: Tzn jeżeli o to chodziło ..

Bogdan: Timie, w zadaniu 5 nie o to chodziło. Podam inne rozwiązanie zadania 3: 129 + 438 = 567

AS: Nie,zadanie błędnie rozwiązane. Chodzi o przedstawienie w postaci wielomianu,gdzie podstawą jest x + 1.

tim: Podstawa wielomianu? (Co to? )

Bogdan: Zad. 5 Wielomian W(x) = x³ + 4x² + 6x + 4 nie tyle rozłożyć, co przedstawić z podstawą: x + 1. Wystarczy wyznaczyć V(x) = W(x − 1) = (x − 1)³ + 4(x − 1)² + 6(x − 1) + 4. Po wykonaniu działań i uporządkowaniu otrzymujemy: V(x) = x³ + x² + x + 1. To jest szukany wielomian. W(x) = V(x + 1) Sprawdzenie: V(x + 1) = (x + 1)³ + (x + 1)² + (x + 1) + 1 ⇒ V(x + 1) = x³ + 4x² + 6x + 4

tim: Ok. Już wiem.

Bogdan: Zadanie 2 w mojej ocenie jest najciekawsze w tym zbiorze pięciu zadań Asa. Szukana liczba naturalna z jedynką na pierwszym miejscu to: y = 10ⁿ⁻¹ + x, gdzie n to liczna cyfr liczby y. Ostatnią cyfrę liczby y oznaczam literką a. Np., jeśli szukaną liczbą y jest liczba 12345, to y = 10⁴ + 2345, tu x = 2345, a = 5. W tym zadaniu układamy równość:

	10n−1 + x − a
2(10n−1 + x) = a*10n−1 +		/ *10
	10

2*10*10ⁿ⁻¹ + 20x = a*10ⁿ + 10ⁿ⁻¹ + x − a 19x = (10ⁿ − 1) − 19*10ⁿ⁻¹

	10n − 1
x =		*a − 10n−1
	19

	10n − 1
x + 10n−1 =		*a,
	19

	10n − 1
widzimy, że nasza szukana liczba jest równa		*a, w liczniku jest n dziewiątek,
	19

czyli 99999...9, ta liczba jest podzielna przez 19, przy pomocy systemowego kalkulatora wyznaczamy n, okazuje się, że n = 18.

1018 − 1
	= 52 631 578 947 368 421, niezła liczba, prawda?
19

Teraz wyznaczamy ostatnią cyfrę a mnożąc 52 631 578 947 368 421 kolejno przez 2, 3 itd., aż do uzyskania jedynki na początku. 52 631 578 947 368 421 * 2 = 105 263 157 894 736 842 Jest jedynka na pierwszym miejscu. Jeśli 105 263 157 894 736 842 jest szukaną liczbą y, to 2y powstanie przez przeniesienie dwójki z ostatniego miejsca na początek. 2 * 105 263 157 894 736 842 = 210 526 315 789 473 684, zgadza się. Odp.: 105 263 157 894 736 842

Eta: Dobry wieczór zad 4/ załóżmy ,że α= 90^o to: β + γ= 90^o L= sin 90^o = 1

	2sinβ+γ2*cosβ −γ2		sinβ+γ2
P=		=		=
	2cosβ+γ2*cosβ−γ2		cosβ+γ2

=tg^90o₂ = tg45^o = 1 L=P więc trójkąt jest prostokątny c.b.d.o.

Bogdan: Witaj Eto . Można rozwiązać zadanie 4 bez założenia, że α = 90^o, może ktoś z maturzystów spróbuje.

Eta: Witaj Bogdanie Oczywiście ,że można , poszłam na skróty Mogę podać inny sposób , ale poczekajmy na maturzystów

Eta: Hmmm, nie ma chętnych? 2/sposób ;

	a		b		c
ze wzoru sinusów mamy:		=		=		= 2R
	sinα		sinβ		sinγ

	a		b		c
to: sinα=		∊ sinβ=		∊ sinγ=
	2R		2R		2R

natomias ze wzoru kosinusów mamy:

	a2 +c2 −b2		a2 +b2 − c2
cosβ=		⊂ cosγ=
	2ac		2ab

zatem:

	sinβ + sinγ
sinα =
	cosβ + cosγ

to:

	a		b2R + c2R
		=
	2R		a2 +c2 −b22ac + a2 +b2 −c22ab

to po przekształceniu otrzymamy:

	(b+c)*2abc
a=
	b(a2 +c2 − b2) +c( a2 +b2 − c2)

2bc( b+c) = a²(b+c) +bc( b+c) − ( b³ − c³) 2bc( b+c) = ( b+c)[a² +bc −( b² − bc +c²)] to: 2bc= a² +bc −b² +bc − c² => a² = b² +c² więc trójkąt jest prostokątny , kąt α= 90^o PS; Bogdan masz jeszcze( w zanadrzu) inną wersję ? Pierwszy sposób ,który podałam jest najkrótszym ,jeżeli chodzi o obliczenia

Bogdan: Tak, mam inną wersję.

	sinβ + sinγ
sinα =		i α = 180o − (β + γ) ⇒ sinα = sin(β + γ)
	cosβ + cosγ

	sinβ + sinγ
sin(β + γ) =
	cosβ + cosγ

	β + γ		β + γ		β + γ   β − γ   2sin cos   2   2
2sin		cos		=
	2		2		β + γ   β − γ   2cos cos   2   2

β + γ

1

β + γ

√2

β + γ

√2

cos2

=

⇒ cos

=

lub cos

= −

2

2

2

2

2

2

β + γ
	= 45o ⇒ β + γ = 90o i α = 90o co należało wykazać.
2

	β + γ
lub		= 135o ⇒ β + γ = 270o nie spełnia warunków zadania.
	2

Eta:

AS: Oto moje propozycje rozwiązań zadań Zadanie 1. Wykaż,że funkcja x¹⁰⁰ + a*x + b ma nie więcej niż dwa miejsca zerowe. Wyznaczam ekstremum funkcji f'(x) = 100*x⁹⁹ + a 99 f'(x) = 0 dla x = √−a/100 Jest to jedyne rozwiązanie a więc i jedno ekstremum. Oznacza to,że funkcja może co najwyżej dwa razy przeciąć oś Ox Zadanie 4. Wykazać,że jeżeli dla kątów trójkąta α,β,γ zachodzi związek sinβ + sinγ sinα = −−−−−−−− cosβ + cosγ to trójkąt jest prostokątny. Sposób 1. Załóżmy,że α jest kątem prostym, Wtedy β + γ = 90^o ⇒ γ = 90^o − β , sinγ = cosβ , cosγ = sinβ sinβ + cosβ sinα = −−−−−−−−−−−− = 1 ⇒ α = 90^o cosβ + sinβ Sposób 2 2*sin(β+γ)/2*cos(β−γ)/2 sinα = −−−−−−−−−−−−−−−−−− = tg(β+γ)/2 2*cos(β+γ)/2*cos(β−γ)/2 180 − α sinα = tg−−−−−−−− = tg(90^o − α/2) = ctg(α/2) 2 2*sin(α/2)*cos(α/2) = cos(α/2)/sin(α/2) cos(α/2)*(2*sin²(α/2) − 1) = 0 cos(α/2) = 0 ⇒ α = 180^o odpada 2*sin²(α/2) − 1 = 0 ⇒ sin(α/2) = 1/√2 ⇒ α = 90^o Zadanie 5. Wielomian x³ + 4*x² + 6*x + 4 rozłożyć na wielomian o podstawie x + 1. x³ + 4*x² + 6*x + 4 = A*(x + 1)³ + B*(x + 1)² + C*(x + 1) + D Po uporządkowaniu x³ + 4*x² + 6*x + 4 = A*x³ + (3*A + B)*x² + (3*A + 2*B + C)*x + (A + B + C + D) Porównując współczynniki mamy A =1 , 3*A + B = 4 , 3*A + 2*B + C = 6 , A + B + C + D = 4 A = B = C = D = 1

AS pik: do AS ; od kiedy to, funkcja przecina osi Ox wykres funkcji przecina ośOx

Bogdan: W zapisie 19x = (10ⁿ − 1) − 19*10ⁿ⁻¹ rozwiązania zadania 2 za nawiasem nie wpisałem literki a, powinno być: 19x = (10ⁿ − 1)a − 19*10ⁿ⁻¹.

AS: Od wtedy,gdy pisałem przed śniadaniem i połknąłem wyraz wykres.

AS pik: Świetne wyjaśnienie pozdrawiam i wybaczam ten lapsus