rownanie Krzychu: dla jakich wartości parametru m równanie 9^x−2*3^x+m=0 ma dokładnie jedno rozwiązanie

Eta: (3^x)²−2*3^x+m=0 Δ=0 ⇒ 4−4m=0 ⇒ m= 1

Krzychu: no własnie, a w odpowiedziach mam do tego jeszcze przedział (−∞,0>. mozliwe to?

Eta: 3^x=t , t>0

Ajtek: Dobry wieczór Eta

Krzychu: Eta, nie rozumiem co masz na myśli

Kejt: zastosuj podstawienie..: 3^x=t czyli masz: t²−2t+m=0

Mateusz: A potem jak juz rozwiazesz rownanie kwadratowe pamietaj aby wroci do podstawienia tj do pierwotnego rownania

Krzychu: no ale z tego i tak nie wyjdzie przeciez to co podają w odpowiedziach, czyli: (−∞,0>U{1} prawda?

Kejt: spróbuj..nie odbierzemy Ci tego dreszczyku emocji..

Krzychu: no jak mi wychodzi to 1 i tyle, nie wiem co dalej

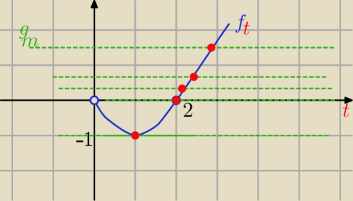
Eta: 3^x=t , t>0 f(t)= t²−2t= t (t−2) −−− patrz wykres i g(m)= −m dla −m=−1 ⇒ m=1 −−− jedno rozwiązanie dla −m≥0 ⇒ m≤ 0 −−− jedno rozwiązanie

Krzychu: a nie da się tego algebraicznie? tego drugiego

pigor: ...otóż, dane równanie 3^2x−2*3^x+m=0 ma dokładnie 1 rozwiązanie ⇔ ⇔ Δ=4−4m=0 (1 podwójny) lub Δ=4−4m>0 i c=m ≤ 0 (2 pierwiastki : 3^x>0 i 3^x<0, czyli różnych znaków, lub jeden 3^x=0 i 3^x<0) ⇔ m=1 lub m<1 i m ≤0 ⇔ ⇔ m=1 lub m ≤ 0 ⇔ m∊(−∞;0> U {1} . ...

Krzychu: pigor, ale nie rozumiem tego toku myślenia. Mamy równanie kwadratowe t²−2t+m=0 i mamy sprawdzić kiedy dla t>0 ma jedno rozwiązanie. To jak delta >0?

Aga1.: Jeśli równanie t²−2t+m=0 ma dwa pierwiastki różnych znaków (Δ>0, t₁*t₂<0 )to równanie 3^x=t, ma jedno rozwiązanie