okrąg Pola: Mamy okrąg o środku w punkcie S=(1,1), kóry odcina na prostej o równaniu x−y+4=) cięciwę o długości 2√2. Znajdź długość promienia okręgu. Wiem, że wszystko trzeba obliczyć, że wzoru (x−a)²+(x−b)²≤r² mamy już x i y, który wynika z punkt, prawda ? a jak obliczyć a i b ? pewnie trzeba jakoś używając to, że mamy podaną cięciwę.

cziki: równanie okręgu ma postać : ( x −a)² + (y −b)² = r² (x−a)² +( y −b)² ≤ r² −−−−− to równanie koła a to jest ogromna różnica ... pamiętaj o tym

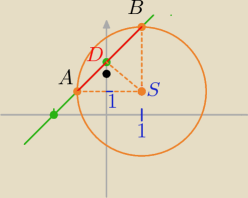
cziki: IABI = 2√2 => IADI= √2 , bo ΔASB jest równoramienny bo ISAI= ISBI = r z ΔADS z tw. Pitagorasa można wyliczyć r = IASI= IBSI zatem:(**) IASI² = IADI² + ISDI² ISDI = d , gdzie d −− jest odległością punktu S od prostej AB pr . AB: x − y +4=0 S( 1,1) więc:

	I1*1 −1*1 +4I
IDSI= d=
	√12 +(−1)2

policz d.... i podstaw do (**) i wyznacz r..... PS; kończę , bo muszę coś zjeść