ttt pause: Dany jest okrąg o równaniu x2 + 4x +y2 − 6y= −5 i prosta l: y=−2x + 1. Wyznacz długość cięciwy okręgu zawartej w danej prostej oraz cosinus kąta środkowego opartego na tej cięciwie. rozwiazalem uklad rownan i wyznaczylem punkty przeciecia prostej z okregem wyznaczylem dlugosc cieciwy ale zawsze jest jakies ale ..... bo nie rozumiem jak autorowi wyszlo cos = −0.8 mi natpomiast wychodzi inaczej nie wiem moze zle to rozumiem ale liczylem to w ten sposob mam punkty A i B ktore sa miejscem przeciecia okregu z prostą i licze dlugosc bokow trojkata czyli odleglosc punktow a A i srodka oraz B i srodka czyli AS i BS wychodzi mi ze jest to trojkat rownoboczny zatem kat ma miare 60 stopni wiec cos = 1/2 nie wiem co zle robie ....

pause: POMOZE KTOSSSS

Tad: chyba pomyliłeś pojęcia kąta środkowego i wpisanego opartych na łuku ...

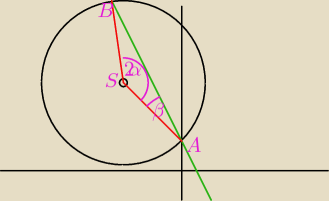
Tad: Rozwiązując układ: równanie okręgu i równanie prostej prostej otrzymasz między innymi A=(0;1) Równanie prostej przechodzącej przez S i A y=−x+1

	−2+1		1
Kąt między prostymi tgβ=|		|=
	1+2		3

tgβ=ctgα

	1		3
Skoro ctgα=		.... to cosα=
	3		√10

cos2α=2cos²α−1 cos2α=−0,8 (2α ... II ćwiartka)