równelogłoboki Emilka: Jak sobie z tym poradzić Kąt ostry w równelogłoboku ma miarę 60 stopni .Odległość punktu przecięcia się przekatnych równelogłobokuod jego boków sa odpowiednio równe 5√3 i 2√3 Oblicz pole i obwód tego równelogłoboku

cziki: pomagam rysuję , cierpliwości ....

imię lub nick.: α = 60

	2h		2h
sinα=		⇒ a =
	a		sinα

	2H		2H
sinα=		⇒ b =
	b		sinα

P=a*b*sinα obw = 2(a+b)

imię lub nick.: ups

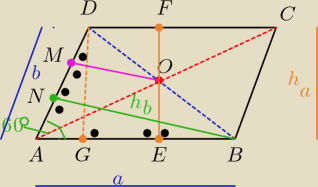cziki: Czy rysunek już Ci pomoże? dodatkowo podpowiadam: IOEI = 2√3 więc h_a= 2*2√3 = 4√3 bo Δ GBD ~ ΔEBO w skali 2:1 ( bo przekątne dzielą się na połowy) podobnie: ΔBDN ~ ΔOMD => że h_b= 2*5√3= 10√3 gdzie: IMOI= 5√3 z trójkąta prostokątnego AGD z funkcji sin60^o wyliczamy długość boku "b"

	ha
		= sin60o => b = 8 ( policz i tak wyjdzie
	b

Pole P= b*h_b = 8*10√3 = 80√3 [j²] podobnie: P= a*h_a => a*4√3= 80√3 => a = 20 ob = 2a +2b =........ policz już sama

Emilka: dziekuje tylko teraz sie zastanawiam jak to dokonczyc jak to popodstawiac 2*5√3 i 2*2√3 to by były wysokosci i jak dalej z tym sobie poradzic?

Emilka: dziekuje slicznie

cziki: prosto: a = 20 b = 8 P= 80√3 [j²} Ob= 2a +2b = 2*20 +2*8 = 40 +16 = 56 [j]

Basia: Eta znowu rozrabia !

cziki: Hehe