wyznacz skale podobieństwa trójkątów Pati: w trójkącie abc a = (2,2) B= (5,3) C= (2,5) natomiast w trójkącie A₁B₁C₁ A₁ = (−2,4) B₁= (0, −2) C₁ = (4,4) wykaz ze trójkąty są podobne i wyznacz skale podobieństwa

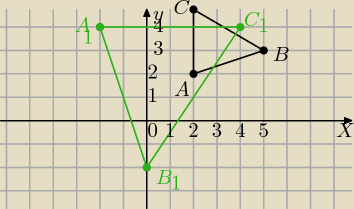
Mila: AB=√3²+1²=√10 AC=3 BC=√2²+3²=√13 A1B1=√2²+6²=√40=2√10=2|AB| A1C1=6=2*|AC| B1C1=√4²+6²=√52=2√13=2|BC| Δ są podobne

	1
ΔABC∼ΔA1B1C1 w skali k=
	2

ΔA1B1C1 ∼ΔABC w skali k=2

Janek191: I AB I = √ ( 5 −2)² + (3 − 2)² = √9 + 1 = √10 I BC I = √ (2 − 5)² + ( 5 − 3)² = √9 + 4 = √13 I AC I = √ (2 − 2)² + (5 − 2)² = √9 = 3 oraz I A₁B₁ I = √ (0 − (−2))² + ( − 2 − 4)² = √ 4 + 36 = √40 = 2 √10 I B₁C₁ I = √ ( 4 −0 )² + (4 − (−2))² = √ 16 + 36 = √52 = 2 √13 I A₁C₁ I = √ ( 4 − (−2))² + (4 − 4)² = √36 = 6 Ponieważ I A₁B₁I / I AB I = 2 ∧ I B₁C₁ I / I BC I = 2 ∧ I A₁C₁ I / I AC I = 2 więc trójkąty: Δ _A1B1C1 i Δ _ABC są podobne Skala podobieństwa k = 2. =====================

Janek191: Pani Milo − proszę zajrzeć na forum/188832.html Chodzi o trapez równoramienny.

Mila: Spojrzałam, napisałam komentarz.