przekształcenia wykresu Cusack: Mam przykładowo funkcję f(x)=3^|x| niech g(x)=3^|x|−2 i h(x)=3^|x−2| Jeżeli wykres funkcji f(x) przesunę o wektor [2,0] to dostanę g(x) czy h(x) ?

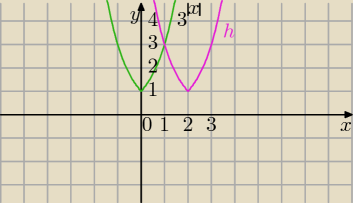
Mila: f(x)=3^|x| translacja o wektor [2,0] ⇒h(x)=3^|x−2|

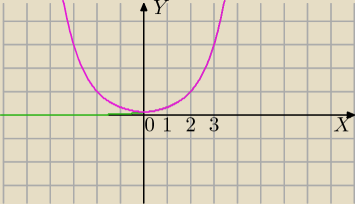
Mila: II g(x)=3^|x|−2 1)y=3^x−2 zielony 2) symetria względem OY prawej części⇒g(x)=3^|x|−2

Cusack: dziękuję. Czyli żeby dostać g(x) to muszę narysować y=3^x−2 dla prawej strony wykresu i zrobić symetrię OY? Ale szczerze powiedziawszy nie za bardzo rozumiem dlaczego właśnie tak...

Cusack: spóźniłem się

Cusack: ale pytanie aktualnie (tylko do g(x)), nie rozumiem dlaczego najpierw 3^x−2 a potem wartosc bezwzgledna na argument. a boje sie ze jezeli nie zrozumiem to za jakis czas to po prostu wyleci i znowu będzie się mylić

Cusack: ?

Mila: Myślę, że najlepiej będzie, gdy rozpiszesz wartość bezwzględną, i oglądaj wykresy.

Mila: 1) Może tak, jeśli w wartości bezwzględnej tylko x, czyli f(|X|), albo jak wolisz we wzorze jest |x|, to rysujesz wykres funkcji, bez wartości bezwzględnej, a potem odbijasz prawą stronę, lewą pomijasz. f(x)=2^|x|+4 f(x) =log₂(|x|+3) f(x)=x²+|x|+5 Rozpisz te przykłady, narysuj wykresy, a potem bez rozpisywania, jak podałam.