. asdf: Twierdzenie Rolle'a Jeżeli funkcja jest ciągła i rózniczkowalna w kazdym punkcie x ∊ (a,b) oraz: f(a) = f(b) to istnieje takie f'(c) = 0, czyli w punkcie c ∊ (a,b) istnieje ekstremum lub funkcja jest stała. Tak na chłopski rozum: jeżeli funkcja na krancach swojego przedziału musi być równa to jeżeli w przedziale (a,b) istnieje takie x₁, że f(x₁) ≠ f(a), czyli w przedziale (a,b) funkcja zmienia swoją monotoniczność (musi wrócić do pierwotnej wartości), tyle wystarczy zrozumieć z tego twierdzenia?

asdf: .

PW: Ja to widzę "obrazkiem". Jeżeli ma na krańcach jednakowe wartości, to gdzieś między a i b wykres ma styczną równoległą do osi OX.

asdf:

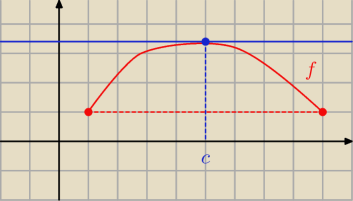
Trivial: Jeśli chodzi o twierdzenie Rolle'a, to jego esencję oddaje obrazek powyżej. f'(c) = 0.

asdf: Tak, rozumiem te twierdzenie, po prostu pytałem czy to co napisalem wyzej wystarczy do tego twierdzenia