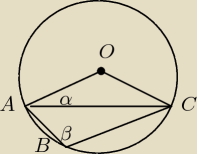
planimetria luzia: Udowodnij, że jeżeli O jest środkiem okręgu, na którym leżą punkty A, B, C, to β= 90^o − α

luzia: podbijam i proszę o pomoc

Janek191: Kąt wklęsły ∡ AOC ma miarę równą 2 β , bo jest kątem środkowym opartym na tej samej cięciwie AC, co kąt wpisany ∡ ABC o mierze β. Dlatego kąt wypukły ∡ AOC ma miarę 360^o − 2β W Δ AOC mamy I AO I = I CO I , więc α + 360^o − 2β + α = 180^o 2 α + 360^o − 180^o = 2 β 2 α + 180^o = 2 β / : 2 β = 90^o + α =============

luzia: dziękuję bardzo, największy problem miałam, żeby zauważyć że wypukły ∡ AOC wynosi 2β a reszta to już z górki