analityczna
Eto": A = (2;1) i B = (4;2) są dwoma kolejnymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne
środka okręgu opisanego na tym kwadracie.
Moj problem polega na tym ze nie moge dojsc ładu z tym zadaniem.
Moge policzyc dlugosc |AB| pozniej nawet dlugosc promienia tego okregu, symetralna odcinka |AB|
jednak nie wiem jak wyznaczxyc te wspolrzedne, prosilbym o rzetelne wytlumaczenie

25 lut 23:14
Mati_gg9225535: jesli masz dlugosc promienia to punkt S jest odległy od prostej AB o długość R, taki wzór z
wart. bezwzględną i pierwiastkiem w mianowniku znajduje sie w karcie wzorów

25 lut 23:27
krystek: Napisz równania prostej AC
Następnie wyznacz współrzędne p C z długości odcinków IABI=IACI i środek okręgu to środek
odc BC
25 lut 23:27
Trivial:
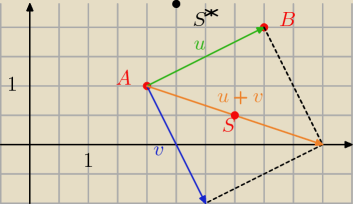
Proponuję zrobić to wektorami.
u = B − A = (2,1)
Wektor v jest prostopadły do u (to jest obrócony o 90
o). Musimy rozważyć dwie możliwości.
Obrót o 90
o oraz o −90
o.
Wzór na obrót wektora u o −90
o (sytuacja z obrazka) jest:
v = (u
y, −u
x) = (1,−2)
| | (2,1) + (1,−2) | | (3,−1) | | 7 | | 1 | |
S = (2,1) + |
| = (2,1) + |
| = ( |
| , |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
Rozważmy drugą możliwość: 90
o (sytuacja przeciwna do obrazka).
v* = −v = (−1,2)
| | (2,1) + (−1,2) | | (1,3) | | 5 | | 5 | |
S* = (2,1) + |
| = (2,1) + |
| = ( |
| , |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
25 lut 23:33
Eta:
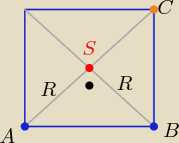
C(x,y)
→ →
AB=[2,1] z prostopadłości wektorów : BC=[1,−2] = [−1,2]
BC=[x−4,y−2]= [1,−2] ⇒ x=5 i y=0
C(5,0)
lub [x−4, y−2]=[−1,2] ⇒ x=3 i y=4
C(3,4)
S jest środkiem odcinka AC to
| | 2+5 | | 1+0 | | 7 | | 1 | | 5 | | 5 | |
S( |
| , |
| ) to S( |
| , |
| ) lub S( |
| , |
| ) |
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |

26 lut 00:31
Eta:
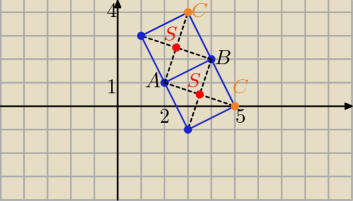
26 lut 00:38


 Proponuję zrobić to wektorami.
Proponuję zrobić to wektorami.
 C(x,y)
→ →
AB=[2,1] z prostopadłości wektorów : BC=[1,−2] = [−1,2]
BC=[x−4,y−2]= [1,−2] ⇒ x=5 i y=0 C(5,0)
lub [x−4, y−2]=[−1,2] ⇒ x=3 i y=4 C(3,4)
S jest środkiem odcinka AC to
C(x,y)
→ →
AB=[2,1] z prostopadłości wektorów : BC=[1,−2] = [−1,2]
BC=[x−4,y−2]= [1,−2] ⇒ x=5 i y=0 C(5,0)
lub [x−4, y−2]=[−1,2] ⇒ x=3 i y=4 C(3,4)
S jest środkiem odcinka AC to

