Jak to zrobić? Marcin212: Wyznacz równanie okręgu o promieniu 3√5 przechodzącego przez punkty A(2,1)B(2,−5)

Tad: (x−x_s)²+(y−y_s)²=r² ... podstawiaj kolejno współrzędne punktów i z układu równań policzysz współrzędne środka okręgu

Marcin212: x i y mam wziąć z równania odcinka AB?

Tad: współrzędne punktów A a potem B

Marcin212: Dziękuję

Marcin212: Ted jesteś tam jeszcze? Stanąłem przy wyliczaniu y0 Ja nie wiem możesz mi to rozpisać ? proszę lub ktoś inny

Tad: (2−x_s)²+(1−y_s)²=45 (2−x₂)²+(−5−y_s)²=45 (1−y_s)²=(−5−y_s)² ... ⇒y_s=−2 podstawiając do pierwszego (2−x_s)²+(1+2)²=45 (2−x_s)²=36 otrzymasz x_s1=−4 x_s2= 8

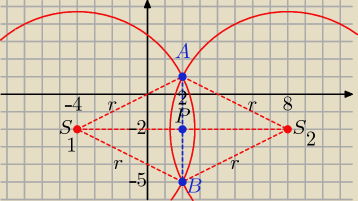
Eta: Są dwa takie okręgi S₁(−4,−2) i r=3√5 to r²=45 S₂(8,−2) i r=3√5 , r²=45 1 sposób |AS|=|BS|=r ⇒ |AS|²=|BS|²=r²=45 , S(x,y) (x−2)²+(y−1)²=(x−2)²+(y+5)² ⇒ (y−1)²=(y+5)² ⇒ 12y=−24 ⇒y=−2 to: (x−2)²+(−3)²= 45 ⇒ (x−2)²= 36 ⇒ x−2=6 v x−2= −6 x=8 v x= −4 S₁(−4,−2) , S₂(8,−2) o₁: ( x+4)²+(y+2)²=45 i o₂: (x−8)²+(y+2)²=45 Na rysunku masz potwierdzenie