boosh...
KevyB: hejo, mam takie glupie zadanie do rozwiazania, tudzież musze narysowac wykres funkcji y=3x2 −
2x − 1
sęk w tym, że kiedy obliczam wierzchołek, wychodzi mi ≈0,33
i niewiem jakie dobrać do tego pozostałe argumenty żeby narysować parabole...
−K
13 sie 17:37
tim: Może to ci pomoże

3x
2 − 2x − 1 = 3x
2 − 3x + x − 1 = 3x(x − 1) + 1(x − 1) = (3x + 1)(x − 1)
Można oliczyć łatwo miejsca zerowe:
(3x + 1)(x − 1) = 0
3x + 1 = 0 x − 1 = 0
3x = −1 x = 1
13 sie 17:39
tim: I nie wolno zaokrąglać, a wierzchołek jest punktem o dwóch współrzędnych

13 sie 17:42
KevyB: ze wzoru na wierzchołki, czyli dla xw = −b/2a a dla yw = −Δ/4a troche inaczej wychodzi, tzn xw
jest 1/3, fakt ale yw jest 4/3 . Strasznie głupie liczby ma to zadanie... znowu z głowy sobie
wzięła
13 sie 17:46
tim: Już sprawdzę.
| | 4 | |
Tak, − |
| wyjdzie, policzyłem −√Δ... |
| | 3 | |
13 sie 17:48
tim: A żeby narysować wykres podstawiaj kolejne liczby i tak oś będzie musiała być co 1/3.
13 sie 17:49
KevyB: | | 1 | | 4 | |
czyli W( |
| ; − |
| ) ? i tak beznadziejne liczby bo rysowac to teraz to jest meczarnia.. |
| | 3 | | 3 | |
13 sie 17:50
Eta:
Wybierz jednostkę 3−y kratki i po strachu

13 sie 17:52
Eta: przyjmij za jednostkę trzy małe kratki

13 sie 17:53
tim:
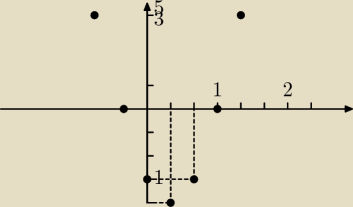
Tak dokładnie. W jest takie jak podałeś. Nie będzie źle.
13 sie 17:55
KevyB: a jakie X przyjąłeś? bo moje to zupełnie źle wychodzi...
13 sie 18:00
KevyB: ja sobie przyjąłem −1/3 , 1/3 i 1, jeszcze raz przelicze
13 sie 18:01
tim: Jak widać u mnie na obrazku, takie same

13 sie 18:04
KevyB: no fakt, tylko ze mam 2 punkty mniej

13 sie 18:04
KevyB: neich zgadne, wziąłeś jeszcze −1 i 1 2/3
13 sie 18:05
tim: Widzisz wykres wyżej?

, jedna kreska to 1/3.
13 sie 18:06
KevyB: aight, a np takie, y = −9x
2 + 12x − 4
| | −b | | 2 | |
delta = 0, jedno miejsce zerowe, więc odrazu jest to też xw, |
| , a więc − |
| |
| | 2a | | 3 | |
dobrze mysle?
13 sie 18:13
tim: Dobry tok rozumowania, ale zły wynik (mała usterka)
13 sie 18:17
KevyB: −b = −12
2a = −18
| | 12 | | 2 | |
− |
| po skroceniu przez 6 = − |
| przecież, czy nie? |
| | 18 | | 3 | |
13 sie 18:19
tim: | −12 | |
|  Minusy się skrócą i zostanie 2/3. |
| −18 | |
13 sie 18:20
123: Nie chce zakładac nowego tematu, tutaj się spytam
czy odcinek łączący ramiona trapezu jest równy
d=√a*b
gdzie:
a i b długości podstaw.
13 sie 18:23
tim: Odcinek łączący ŚRODKI ramion trapezu?

Jeżeli tak, to
d = a + b / 2
13 sie 18:25
123: hah, właśnie też obliczyłem jak ty, ale jednak nie z tego zostało te coś wzięte, mniejsza z
tym, dzięki

13 sie 18:27
tim: Trzeba być dociekliwym a nie!

, już się poddajesz..

13 sie 18:28
KevyB: | | 1 | |
dla 1 |
| funkcja przyjmuje wartość 4? |
| | 3 | |
13 sie 18:29
tim: Ahh.. Nie, −4.
13 sie 18:30
KevyB: fu fakt, −4, minusa nie wcisnalem dx
13 sie 18:31
tim: Uff..

13 sie 18:31
KevyB: dobra, rozwalil mi sie dlugopis na kawalki bo wystrzelil nagle, ide po nowy i przy okazji cos
zjesc bo zwariuje, juz caly dzien tluke kazdy rodzaj tematu, cholerna poprawka, a raczej
klasyfikacyjny... bo moja wina ze bylem cholera chory czesto −.−
13 sie 18:31
123: Tim, już wiem skąd się tamto coś wzieło, dobrze że nie dodałem tutaj tego zadania...głupka bym
z siebie tylko zrobił^^
13 sie 18:32
tim: Ale powiedz
 http://www.jogle.pl/wykresy/
http://www.jogle.pl/wykresy/ − może to ci coś pomoże...
KevyB − spokojnie, jutro będzie nowy dzień, jak to mawia Eta:
* optymizm! to podstawa sukcesu!
* Pamiętaj : " co Cie nie zabije, to Cię wzmocni"
* przez kłopoty stajemy sie silniejsi
13 sie 18:35
KevyB: Cholera nie chce mi wyjść −4 jak robie z 1U{1}[3}
| | 1 | | 1 | | 10 | |
Potęguje 1 |
| i wychodzi mi 1 |
| , upraszczam na |
| |
| | 3 | | 9 | | 9 | |
| | 9 | | 10 | |
więc, − |
| * |
| skracam 9tki i mam −10 |
| | 1 | | 9 | |
| | 1 | | 12 | | 4 | | 4 | | 4 | |
a 12 * 1 |
| = |
| * |
| skracam 12 z 3 i mam 4 , więc |
| * |
| = 16 |
| | 3 | | 1 | | 3 | | 1 | | 1 | |
−10 + 16 − 4 wychodzi mi 2
gdzie siedzi ten błąd −.−'
13 sie 18:47
KevyB: | | 1 | |
chyba w potęgowaniu 1 |
| |
| | 3 | |
13 sie 18:49
KevyB: ta, zapomniałem tego uprościć przed potęgowaniem −.−, nieważne już d;
13 sie 18:50
tim: I widzisz

13 sie 18:50
KevyB: a w −x2 + 6x − 5 to W(3 ; 4) ?
13 sie 18:56
tim: Tak.
13 sie 18:58
KevyB: no dobra ale biore sobie takie X
0 , 3 i 6
0 fajnie wychodzi −5 , dla 3 już 22 a dla 6 wychodzi wogole 67, cos mi tu nie pasuje...
odleglosc jest taka sama przeciez, ale Y wogole nie pasuja
13 sie 18:59
tim: To jest funkcja kwadratowa! Pamiętaj. Najlepiej widać to na przykładzie:
y = x2
x = 0 y = 0
x = 1 y = 1
x = 2 y = 4
x = 3 y = 9
x = 4 y = 16
x = 5 y = 25
itd.
13 sie 19:02
KevyB: czyli co , takie punkty są dobre?
f(−3) = −14
f(0) = −5
f(3) = 22
troche krzywa ta parabola >.>
13 sie 19:06
KevyB: to nawet nie jest parabola już
13 sie 19:07
tim: Na pewno to do tej funkcji jest? Podaj wzór funkcji.
13 sie 19:09
KevyB: −x2 + 6x − 5
13 sie 19:11
13 sie 19:16
Bogdan:
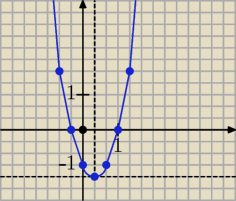
Dzień dobry.
y = 3x
2 − 2x − 1
Δ = 4 + 12 = 16,
√Δ = 4
| | 2 − 4 | | 1 | | 2 + 4 | |
Miejsca zerowe: x1 = |
| = − |
| , x2 = |
| = 1 |
| | 6 | | 3 | | 6 | |
Na rysunku obieramy taką skalę na osiach układu współrzędnych, której jednostka jest
| | 1 | | 4 | |
równa trzem "kratkom", 3 kratki = 1, jedna kratka = |
| , 4 kratki = |
| , itd. |
| | 3 | | 3 | |
13 sie 19:18
tim: Witaj Bogdanie. Do tego już doszliśmy.
13 sie 19:19
KevyB: a nie, dla f(3) fakt, 22, ale dla f(−3) juz nie.
−32 + 6 * (−3) −5 = 9 −18 − 5 = −14 , gdzie tu jest błąd o.o
kwadratowany minus = plus (tak długo jak parzysty kwadrat)
−3 * −3 = 9
6 * (−3) = −18
i to wszystko −5 = −14
13 sie 19:21
tim: Mamy − (x2) = − (−3)2 = − (9) = −9
13 sie 19:23
tim:

13 sie 19:25
tim:
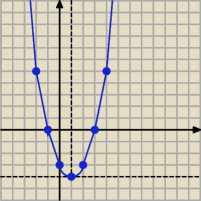
13 sie 19:33
tim: Też tak umiem

13 sie 19:34
KevyB: no dobra ale to wtedy i tak jest dziwne
bo −9 − 18 [6 * (−3)] − 5 , wychodzi jeszcze mniej o.0
13 sie 19:44
KevyB: a nie zaraz, dobrze, mi sie ze wczesniejszym 4 pomerdało dx
13 sie 19:45
tim: 
13 sie 19:47
KevyB: dobra , a naprzykład takie coś, mam polecenie "Wyznacz najmniejsze i największe wartości
funkcji w przedziale:"
i
y=4x2 − 4x − 3 dla <−1,0> , i <1,3>
jak do tego podejść? coś mi tam świta ale tak niepewnie..
13 sie 19:53
KevyB: a i "wyznacz najmniejsze i największe wartości tych funkcji w całej dziedzinie"
13 sie 19:55
Eta:
y= 4x
2 −4x −3 dla x€R ( czyli w całej dziedzinie)
| | −b | |
osiąga tylko minimum dla xw= |
|
|
| | 2a | |
| | −Δ | |
ymin= yw= |
| .... policz tę wartość
|
| | 4a | |
bo a>0 i ramiona paraboli zwrócone do góry
1/ gdy x€< −1,0>
x=
12 nie nalezy do tego przedziału
więc : policz y( −1) =..... i y(0) =.....
i podaj odp: mniejsza wartość minimum , większa to maximum w tym przedziale.
dla x€< 1, 3> x
W=
12 też nie należy do tego przedziału
więc policz .... podobnie y(1) =... i y(3)=....
14 sie 00:13
 3x2 − 2x − 1 = 3x2 − 3x + x − 1 = 3x(x − 1) + 1(x − 1) = (3x + 1)(x − 1)
Można oliczyć łatwo miejsca zerowe:
(3x + 1)(x − 1) = 0
3x + 1 = 0 x − 1 = 0
3x = −1 x = 1
3x2 − 2x − 1 = 3x2 − 3x + x − 1 = 3x(x − 1) + 1(x − 1) = (3x + 1)(x − 1)
Można oliczyć łatwo miejsca zerowe:
(3x + 1)(x − 1) = 0
3x + 1 = 0 x − 1 = 0
3x = −1 x = 1



 Tak dokładnie. W jest takie jak podałeś. Nie będzie źle.
Tak dokładnie. W jest takie jak podałeś. Nie będzie źle.


 , jedna kreska to 1/3.
, jedna kreska to 1/3.
 Minusy się skrócą i zostanie 2/3.
Minusy się skrócą i zostanie 2/3. Jeżeli tak, to
d = a + b / 2
Jeżeli tak, to
d = a + b / 2

 , już się poddajesz..
, już się poddajesz.. 

 http://www.jogle.pl/wykresy/ − może to ci coś pomoże...
KevyB − spokojnie, jutro będzie nowy dzień, jak to mawia Eta:
* optymizm! to podstawa sukcesu!
* Pamiętaj : " co Cie nie zabije, to Cię wzmocni"
* przez kłopoty stajemy sie silniejsi
http://www.jogle.pl/wykresy/ − może to ci coś pomoże...
KevyB − spokojnie, jutro będzie nowy dzień, jak to mawia Eta:
* optymizm! to podstawa sukcesu!
* Pamiętaj : " co Cie nie zabije, to Cię wzmocni"
* przez kłopoty stajemy sie silniejsi

 Dzień dobry.
y = 3x2 − 2x − 1
Dzień dobry.
y = 3x2 − 2x − 1



