Cosinus kąta alfa Stach: Witam, chciałbym poprosić o rozwiązanie zadania: http://i.imgur.com/AKnlAC4.png Uwzględniając dane przedstawione na rysunku, wykaż, że:

	2√ab
cos α =
	a+b

Mila:

	a		b		a		b
sinα=		i sinα=		⇔		=		stąd
	OA		OA+(a+b)		|OA|		|OA|+(a+b)

	a(a+b)
|OA|=
	b−a

	b−a		b2−2ab+b2
sinα=		⇔sin2α=
	a+b		(a+b)2

cos²α=1−sin²α⇔

	b2−2ab+b2		(a+b)2−b2−2ab+b2
cos2α=1−		=
	(a+b)2		(a+b)2

	4ab
cos2α=
	(a+b)2

	2√ab
cosα=
	a+b

cnw

Stach: Dobra, dziękuję.

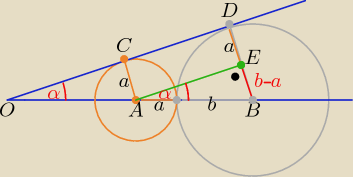
Eta: z trójkąta prostokątnego ABE

	b−a		(b−a)2
sinα=		⇒ sin2α=
	a+b		(a+b)2

i dalej już tak jak policzyła Mila

Mila: Witaj, Eto, nie chciało mi się rysować, to musiałam więcej liczyć. Pozdrowienia