h peccatoribus : Dana jest funkcja f(x) = xe^1/x Chcę zbadać jej monotoniczność. Liczę pochodną, sprawdzam dziedziny f(x) i f'(x) − są sobie równe.

	e1/x(x−1)
Rozwiązuję równanie f'(x) = 0 ⇔		= 0 Rozwiązaniem jest x = 1.
	x

Rysuję przybliżony wykres. Odczytuję: f↘: x ∊ (−∞; 0) ∪ (0; 1) f↗: x ∊ (1; ∞) minL(1; e) Nie wiem gdzie popełniłem błąd ale w rozwiązaniu mam: f↘ x ∊ (0;1) f↗ x ∊ (−∞;0) ∪ (1;∞). Proszę o pomoc.

rozi: w odpowiedziach jest jakby wykres szedł od drugiej strony ale wg. mnie jest ok.

peccatoribus : No właśnie... ale chyba jednak błąd jest po mojej stronie bo to rozwiązanie z etrapeza a tam chyba jednak tylu ludzi liczyło, że ew. błędy poprawili . Ktoś pomoże?

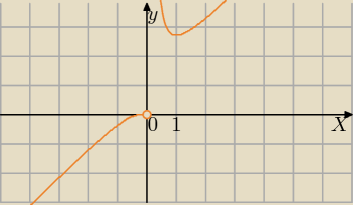Mila: 1) f(x) = xe^1/x, x≠0 f '(x)=0⇔x=1 wtedy f(1)=e Monotoniczność− Badamy znak pochodnej f'(x)>0⇔x(x−1)>0⇔x<0 lub x>1 zatem f(x)↗ (rosnaca) dla x<0 lub x>1 f(x)↘ dla x∊(0,1) w punkcie x=1 ma minimum, pochodna rowna 0 i pochodna zmienia znak przy przejsciu przez punkt x=1 Jeśli dalej masz pytania , to pisz.