trapez + funkcja liniowa
ewe7: Punkty A=(2,0) B=(8,3) C=(7,4) są kolejnymi wierzchołkami trapezu równoramiennego o podstawie
AB. Wyznacz współrzędne wierzchołka D tego trapezu.
Prosze o rozwiązanie
24 lut 19:41
krystek:
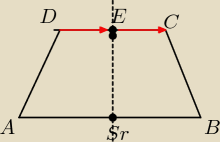
1Napisz r−nie prostej AB
2)Prostej DC
3) wyznacz Srodek Sr (odcinka AB)
4) Napisz równanie ESr
5 w przecięciu prostej ESr i CD leży punkt E i teraz wektor EC→=DE→
24 lut 20:17
Janek191:
A = ( 2; 0), B = ( 8; 3), C = ( 7; 4)
Niech
D = ( x; y)
pr AB :
y =ax + b
0 = 2a + b
3 = 8a + b
−−−−−−−−−−−−−− odejmujemy stronami
3 = 6a
a = 1/2
−−−−−−−−
b = − 2a = − 2*0,5 = − 1
−−−−−−−−−−−−−−−−
y = 0,5 x − 1 − równanie prostej AB
=============
pr CD jest równoległa do pr AB i przechodzi przez C :
wiec
y = 0,5 x + b
4 = 0,5*7 + b
4 − 3,5 = b
b = 0,5
−−−−−−−
y = 0,5 x + 0,5 − równanie prostej CD
=============
S − środek odcinka AB :
xs = ( 2 + 8)/2 = 5
ys = ( 0 + 30/2 = 1,5
S = ( 5; 1,5 )
=============
Symetralna odcinka AB i równocześnie symetralna odcinka CD przechodzi przez S
i jest prostopadła do pr AB, zatem
0,5 *a2 = − 1 ⇒ a2 = − 2 i S = ( 5; 1,5)
więc
y = −2 x + b2
1,5 = −2*5 + b2
1,5 + 10 = b2
b2 = 11,5
−−−−−−−−−−−−
y = −2 x + 11,5 − równanie symetralnej odcinka AB
=============
Szukam środka odcinka CD − punkt przecięcia się pr CD z symetralną odcinka AB :
y = 0,5 x + 0,5
y = −2 x + 11,5
−−−−−−−−−−−−−−−−−−−
0,5 x + 0,5 = −2x + 11,5 / * 2
x + 1 = − 4x + 23
5x = 22
x = 4,4
−−−−−−−
y = 0,5*4,4 + 0,5 = 2,2 + 0,5 = 2,7
−−−−−−−−−−−−−−−−−−−−−−−−−−−
S1 = ( 4,4 ; 2,7 ) − środek odcinka CD
=================
D = ( x; y)
C = ( 7; 4)
S1 − środek odcinka CD
więc
( 7 + x)/2 = 4,4
( 4 + y)/2 = 2,7
−−−−−−−−−−−−−−−
7 + x = 8,8
4 + y = 5,4
−−−−−−−−−
x = 1,8
y = 1,4
−−−−−
Odp. D = ( 1,8 ; 1,4 )
=====================
24 lut 20:35
Bogdan:
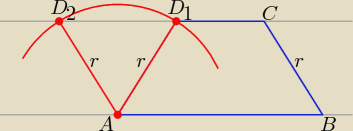
Są 2 rozwiązania spełniające warunki zadania: trapez ABCD
1 oraz trapez ABCD
2
r
2 = (7 − 8
2 + (4 − 3)
2 = 2,
| | 3 − 0 | | 1 | |
prosta AB: y = a1x + b1, a1 = |
| = |
| |
| | 8 − 2 | | 2 | |
| | 1 | | 1 | | 1 | |
prosta CD: y = a2x + b2, a1 = a2 = |
| , y = |
| (x − 7) + 4 ⇒ y = |
| x + |
| | 2 | | 2 | | 2 | |
24 lut 20:51
Eta:

24 lut 20:53
Bogdan:
| | 1 | | 1 | |
prosta CD: y = |
| x + |
| |
| | 2 | | 2 | |
okrąg o środku A i promieniu r: (x − 2)
2 + y
2 = 2
Po rozwiązaniu tego układu równań otrzymamy współrzędne punktów D
1 i D
2
24 lut 20:53
Bogdan:
mały chochlik zjadł nawias, poprawiam: r2 = (7 − 8)2 + (4 − 3)2 = 2
24 lut 20:55
Janek191:
Do Bogdana : Jakiś dziwny ten II trapez równoramienny !
24 lut 21:15
Bogdan:
A co w nim dziwnego? Trapez to trapez, czyli czworokąt wypukły, który ma 2 boki równoległe,
równoległobok też jest przecież trapezem.
24 lut 21:35
Janek191:
Def. 14.5
a) Trapezem nazywamy czworokąt mający przynajmniej dwa boki równoległe ;
trapez mający dwa boki przeciwległe nierównoległe i równe nazywamy równoramiennym.
Patrz. GEOMETRIA dla klasy I technikum. Zofia Krygowska, Janina Maroszkowa.
PZWS 1969 strona 105.
24 lut 21:48
Bogdan:
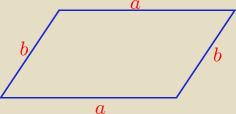
Czy ten trapez
Janku191 jest równoramienny? Jeśli tak, to spełnia warunki zadania.
24 lut 21:59
pigor: ... , Punkty A=(2,0) B=(8,3) C=(7,4) są kolejnymi wierzchołkami trapezu
równoramiennego o podstawie AB. Wyznacz współrzędne wierzchołka D tego trapezu.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
no to może jeszcze np. tak :niech
(x,y)=D − szukany
wierzchołek, to
z własności trapezu równoramiennego :
AB
→ || CD
→ i |AD
→|= |BC
→| ⇔ [6,3] || [x−7,y−4] i AD
2= BC
2 ⇔
⇔
6x−7 =
3y−4 i (x−2)
2+y
2=1
2+(−1)
2 ⇔ 2(y−4)= x−7 i (x−2)
2+y
2=1=2 ⇔
⇔
x=2y−1 i (2y−3)
2+y
2−2=0 ⇒ 5y
−5y−7y+7=0 ⇔ 5y(y−1)−7(y−1)=0 ⇔
⇔ (y−1)(5y−7)=0 ⇔
y=1 ∨
y= 75 ⇒
⇒
(x,y)= (1,1}=D ∨
(x,y)= (95,75)=D . ... 
25 lut 00:10
Janek191:
Do Bodana : To nie jest trapez równoramienny , ale równoległobok.
Definicję trapezu równoramiennego podałem wyżej. Trapez równoramienny
ma jedna parę boków równoległych .
25 lut 07:56
Janek191:
Do pigora − też nie znasz definicji trapezu równoramiennego ?
25 lut 07:58
Janek191:
Trapez równoramienny
www.bazawiedzy.com ( materiały do nauki matematyki ... )
oraz Wikipedia
25 lut 08:12
Bogdan:
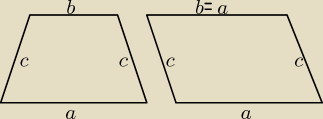
Oj
Janek191 
nie chce mi się już więcej przekonywać Ciebie, że równoległobok
jest też trapezem i to równoramiennym. Jeśli dalej tkwisz w przekonaniu, że jest inaczej, to
trudno.
25 lut 11:05
pigor: ... cóż, ten typ tak ma i ciężko z nim polemizować , mylisz kolego
J... definicję z własnościami, ano i niech ci już tak będzie , amen . ...

25 lut 12:17
pigor: ...., a czworokąt kolegi
B... to oczywiście trapez równoramienny, który
nazwano z powodu swoich dodatkowych własności, równoległobokiem i tyle .

25 lut 12:43
Janek191:
Widzę, że czytanie ze zrozumieniem nie jest Waszą mocną stroną.
W definicji prof. dr hab. Zofii Krygowskiej wyraźnie napisano, że trapezem
równoramiennym nazywamy trapez , w którym boki nierównolegle są równe.
W równoległoboku ( który też jest trapezem) są dwie pary boków równoległych,
zatem nie może być trapezem równoramiennym.
25 lut 15:22
Eta:
| | a+b | | a+a | |
P(trapezu)= |
| *h = |
| *h=a*h=P(równoległoboku) |
| | 2 | | 2 | |

25 lut 15:48
Bogdan:
Jednak muszę zabrać głos jeszcze raz.
Jeśli ograniczymy się do stwierdzenia: "w trapezie równoramiennym ramiona są równej
długości", to równoległobok, romb, prostokąt i kwadrat są takim trapezem.
Jeśli uzupełnimy stwierdzenie "w trapezie równoramiennym ramiona są równej długości"
o warunek: " i miary kątów wewnętrznych przy podstawie są równe"
lub
"i przekątne są równej długości"
lub
"i trapez posiada oś symetrii przechodzącą przez środki podstaw"
to równoległobok i romb nie są trapezami równoramiennymi, natomiast prostokąt i kwadrat tak.
W tych ostatnich trzech przypadkach rację ma Janek191
25 lut 17:18
Bogdan:
Myślę, że w przypadku takich zadań trzeba w rozwiązaniu podać przyjęte kryteria opisujące
badaną figurę.
25 lut 17:20
pigor: ..., cóż, to raczej ty nie potrafisz czytać ze zrozumieniem i radzę jeszcze raz przeczytać
o czym piszę, a co do twojego sposobu rozwiązania powyższego zadania wolę się
nie wypowiadać, no ale jeśli na stronie ... zadane., czy coś tam , tak się rozwiązuje
zadania to ... współczuję wszystkim, którzy korzystają z niej .

25 lut 18:30
Mila:
Niektórzy autorzy definiują trapez jako czworokąt posiadający tylko jedną parę boków
równoległych, tzn. uważają, że równoległobok nie jest trapezem.
Z trapezem w praktyce szkolnej było trochę bałaganu, jednak obowiązująca od dość dawna
definicja:
Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych.
Definicja trapezu równoramiennego to problem wielu podręczników.
Trapez równoramienny jest to trapez, mający oś symetrii, przechodzącą przez środki podstaw (i
będącą zarazem ich symetralną). Ramiona takiego trapezu są równej długości. Kąty między
ramionami a daną podstawą są sobie równe.
Jednak dalej bałagan trwa.
I dlatego w podanym zadaniu rację ma i Janek i Bogdan, wszystko zależy od przyjętej definicji.
Autor zadania, powinien treść doprecyzować.
U Kurczaba, jest w zadaniu sformułowanie z osią symetrii, to nie ma wątpliwości o co chodzi w
zadaniu, inni piszą, "trapez równoramienny nie będący równoległobokiem".
Kiełbasa:
"Uwaga: Przyjmujemy,że równoległobok nie jest trapezem równoramiennym"
27 lut 19:00
 1Napisz r−nie prostej AB
2)Prostej DC
3) wyznacz Srodek Sr (odcinka AB)
4) Napisz równanie ESr
5 w przecięciu prostej ESr i CD leży punkt E i teraz wektor EC→=DE→
1Napisz r−nie prostej AB
2)Prostej DC
3) wyznacz Srodek Sr (odcinka AB)
4) Napisz równanie ESr
5 w przecięciu prostej ESr i CD leży punkt E i teraz wektor EC→=DE→
 Są 2 rozwiązania spełniające warunki zadania: trapez ABCD1 oraz trapez ABCD2
r2 = (7 − 82 + (4 − 3)2 = 2,
Są 2 rozwiązania spełniające warunki zadania: trapez ABCD1 oraz trapez ABCD2
r2 = (7 − 82 + (4 − 3)2 = 2,

 Czy ten trapez Janku191 jest równoramienny? Jeśli tak, to spełnia warunki zadania.
Czy ten trapez Janku191 jest równoramienny? Jeśli tak, to spełnia warunki zadania.

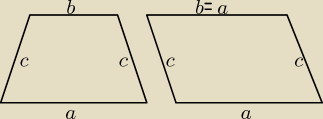 Oj Janek191
Oj Janek191  nie chce mi się już więcej przekonywać Ciebie, że równoległobok
jest też trapezem i to równoramiennym. Jeśli dalej tkwisz w przekonaniu, że jest inaczej, to
trudno.
nie chce mi się już więcej przekonywać Ciebie, że równoległobok
jest też trapezem i to równoramiennym. Jeśli dalej tkwisz w przekonaniu, że jest inaczej, to
trudno.



