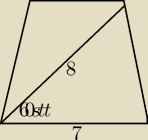
Trapez i równoległobok. Pierwiastek: Zad. 1. Oblicz pole trapezu równoramiennego przedstawionego na rysunku. Tam gdzie jest kąt to pise 60 stopni Zad. 2. Pole równoległoboku o kącie ostrym 30 stopni wynosi 16, a jeden z boków jest dwukrotnie dłuższy od drugiego boku. Wyznacz obwód tego równoległoboku oraz wysokość między parą boków krótszych . Stanęłam na rysunku Mógłby mi ktoś wytłumaczyć ?

Janek191: z.1 h − wysokość trapezu Mamy h −− = sin 60^o = √3/2 / * 8 8 h = 4 √3 ========== a = 7 b = ? Mamy x + b + x = a = 7 Mamy ( 7 −x)² + h² = 8² wiec 49 − 14x + x² + ( 4 √3)² = 64 x² − 14 x + 49 + 48 − 64 = 0 x² − 14 x + 33 = 0 −−−−−−−−−−−− Δ = ( −14)² − 4*1*33 = 196 − 132 = 64 √Δ = 8 x = ( 14 − 8)/2 = 3 lub x = ( 14 + 8)/2 = 11 > 7 − odpada b = a − 2x = 7 − 2*3 = 1 −−−−−−−−−−−−−−−−−−− Pole trapezu : P = 0,5 *( a + b) *h P = 0,5 *( 7 + 1) * 4 √3 = 16 √3 ============================== Uwaga : Dane do zadania są z " sufitu ".

Janek191: Dane są dobre − zmierzyłem inny kąt niż należało.

Janek191: Dane są dobre − zmierzyłem inny kąt niż należało.

Janek191: a = 2x b = x α = 30^o Pole równoległoboku : P = a*b* sin α czyli P = 2x*x * sin30^o = 2 x² * 0,5 = x² zatem x² = 16 x = √16 = 4 więc a = 2*4 = 8 b = x = 4 Obwód równoległoboku : L = 2a + 2b = 2*8 + 2*4 = 16 + 8 = 24 ================================= P = b*h h − odległość krótszych boków równoległoboku zatem 4h = 16 h = 4 ===========

Pierwiastek: Dziękuję Bardzo dziękuję

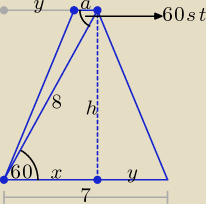
Bogdan: Korzystając z własności trójkąta prostokątnego o kącie ostrym 60^o otrzymujemy od razu: x = 4, y = 3, a = x − y = 1

	1		1		√3
Pole trapezu P=		*7*8*sin60o+		*1*8*sin60o=32sin60o=32*		=16√3
	2		2		2

i tyle