Prawdopodobieństwo - losowy punkt kwadratu leneek: Obliczyć prawdopodobieństwo tego, że wybrany w sposób losowy punkt kwadratu |x| < 1, |y| < 1 jest punktem leżącym wewnątrz okręgu o równaniu x² + y² = 1. Wiem, że okrąg będzie o środku (0, 0) oraz o promieniu 1. Ale jak obliczyć pole kwadratu?

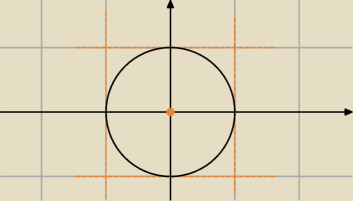
Aga1.: A nie powinno być IxI≤1 i IyI≤1?

leneek: Nie, dobrze jest napisane. A kwadrat ma chyba leżeć wewnątrz okręgu, a nie na zewnątrz, jeśli dobrze rozumiem treść zadania.

Artur_z_miasta_Neptuna: dlaczego krawdat ma leżeć wewnątrz okręgu ... gdyby tak bylo to bez liczenia ... P(A) = 1 bo każdy punkt kwadratu leży wewnątrz okręgu ... a tak nie jest

Aga1.: IxI<1⇔−1<x<1 IyI<1⇔−1<y<1 Rysunek jest poprawnie wykonany. Masz odp?

leneek: Nie bardzo rozumiem. Ale chyba nie będzie tak, jak Aga1 narysowała, bo w poleceniu pisze, że |x|<1 i |y|<1. Więc kwadrat będzie wewnątrz okręgu. A wynik jest taki π/4. Może to w czymś pomoże?

n,ick:

leneek: Z tego wynika, że długość boku kwadratu wynosi 2. To by się zgadzało: πr²/a² = π/4 Ale dalej nie wiem, dlaczego tak?

Artur_z_miasta_Neptuna: niby dlaczego ma być wewnątrz okręgu ... narysuj proste ... x=1 ; x=−1 ; y=1 ; y=−1 wnętrze powstałe przez te proste ... to Twoj kwadrat a okrąg jest wewnątrz tego kwadratu ... bo to okrąg o środku w 0,0 oraz promieniu 1

leneek: Okej, w sumie uważam, że macie racje, a jak wytłumaczycie |x| < 1, |y| < 1? A jeśli będzie, że punkt kwadratu |x| < 1, |y| < 1 jest punktem leżącym na zewnątrz okręgu o równaniu x² + y² = 1?

Trivial: To wtedy interesuje Cię część powstała przez wycięcie z tego kwadratu koła.

	pole kwadratu   pole koła   −
P =		=
	pole kwadratu

	pole koła
= 1 −
	pole kwadratu

Mila: LIczysz prawdopodobieństwo zdarzenia punkt należy do kwadratu i do koła Ω − zbiór wszystkich punktów kwadratu A− część wspólna kwadratu i koła

leneek: Bardzo ogromnie dziękuję, tylko jest błąd w obliczeniu, powinno być: ^π*12_2² = ^π₄

leneek:

π * 12		π
	=
22		4

Mila: Oczywiście 1²=1

Mila: ?

leneek: Witam Mila, teraz nie rozumiem, dlaczego później napisałaś pytajnik? To znaczy, że nie było żadnego błędu?

Mila: Dobrze zauważyłaś, wszystko w porządku, to przypadkowy był post. Pracuj dalej.