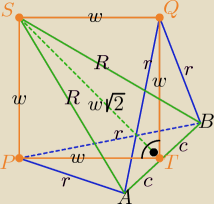
:) pll: Na powierzchni kuli o promieniu R=√313 cm znajdują się dwa jednakowe okręgi, ktorych płaszczyzny są prostopadłe. Wspólna cięciwa AB tych okręgow ma długość 10cm. Oblicz długość promienia r tych okręgów

Bogdan: S − środek kuli o promieniu R, P, Q − środki prostopadłych do siebie okręgów o promieniach r, AB − cięciwa kuli i wspólna cięciwa okręgów o promieniach r Dane: R, |AB| = 2c Szukane: r W trójkącie ATS: (w√2)² + c² = R² ⇒ 2w² = R² − c²

	2R2 − (R2 − c2)
W trójkącie APS: r2 = R2 − w2 ⇒ 2r2 = 2R2 − 2w2 ⇒ r2 =
	2

	R2 + c2
r2 =
	2

pll: Dziękuję

Bogdan: Podaj swoje liczbowe rozwiązanie

Eta: r=13 cm

Bogdan:

Eta: Świetny rysunek Bogdanie Ja miałam rozwiązanie, ale nijak nie wychodził mi tu przejrzysty rysunek Pozdrawiam

Bogdan: Dziękuję Eto. Staram się by rysunki nie odbiegały jakością od pisanej treści rozwiązania. Również pozdrawiam