Wykaż, że miara kątów jest dwukrotnie większa.
Kasia: W trójkącie równoramiennym kąt przy podstawie jest równy α. Wykaż, że symetralne ramion tego
trójkąta tworzą kąt, którego miara jest równa 2α.
24 lut 13:27
Mati_gg9225535:
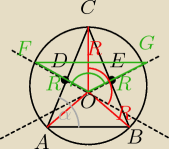
|∡COB| = 2α
ΔCOB
= ΔFOG Zatem |∡FOG| = 2α
24 lut 13:48
Basia:
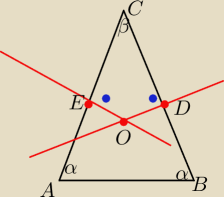
przecież nie o ten kąt chodzi w zadaniu, tylko o ∡EOD
z △ABC
α+α+β = 180
β = 180−2α
|∡CEO| = |∡CDO| = 90 (bo symetralne są prostopadłe do boków)
z □CEOD
β+90+|∡EOD|+90 = 360
180−2α+180+|∡EOD| = 360
|∡EOD| = 2α
co należało udowodnić
29 sty 15:30
 |∡COB| = 2α
ΔCOB = ΔFOG Zatem |∡FOG| = 2α
|∡COB| = 2α
ΔCOB = ΔFOG Zatem |∡FOG| = 2α
 przecież nie o ten kąt chodzi w zadaniu, tylko o ∡EOD
z △ABC
α+α+β = 180
β = 180−2α
|∡CEO| = |∡CDO| = 90 (bo symetralne są prostopadłe do boków)
z □CEOD
β+90+|∡EOD|+90 = 360
180−2α+180+|∡EOD| = 360
|∡EOD| = 2α
co należało udowodnić
przecież nie o ten kąt chodzi w zadaniu, tylko o ∡EOD
z △ABC
α+α+β = 180
β = 180−2α
|∡CEO| = |∡CDO| = 90 (bo symetralne są prostopadłe do boków)
z □CEOD
β+90+|∡EOD|+90 = 360
180−2α+180+|∡EOD| = 360
|∡EOD| = 2α
co należało udowodnić