parametr m i wartość bezwzględna ela: Określ dla jakiej wartości parametru m równanie ||x − 3| − 4| = m ma dwa rozwiązania?

Krzysiek: Ja nie umiem tu rysowac wiec CI nie narysuje . Powiem CI jak to zrobic 1 .Rysujesz wykres tej funkcji f(x)=||x−3|−4| tak a) rysujesz wykres f(x)=(x−3) i przesuwasz go o 4 jednostki w dol −poczytaj o przesuwaniu wykresu wzdluz osi OX i OY b) ale masz to w module wiec musisz ta czesc wykresu ktora jest pod osia OX odbic do gory nad os OX −gdyz z definicji wartosc bezwagledna nie moze byc ujemna . Do tej pory mysle ze zrozumiale 2. Teraz prosta y=m przesuwasz wzdluz osi OY i patrzysz w jakim przedziale ta prosta przetnie wykres f(x)=||x−3|−4| w dwoch miejscach . Piszesz ten przedzial i koniec

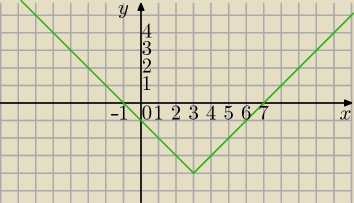
Mila: Y=|x−3|−4 Zaraz resztę narysuję w drugim układzie, abyś zrozumiała co pisze p.t Krzysiek

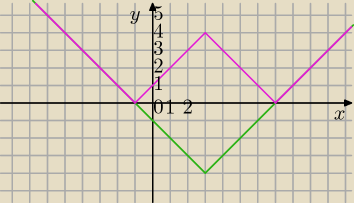
Mila: f(x)=||x−3|−4| różowy wykres. Teraz odpowiedz na postawione pytanie.

ela : {0} dwa rozwiązania

Mila: Rysujesz prostą poziomą np y=0 są dwa rozwiązania y=5 są dwa rozwiązania czyli ||x−3|−4| =m ma dwa rozwiązania dla m=0 lub m>4