 f '(x)=15x4−60x2
15x4−60x2=0
15x2(x2−4)=0
x=0 (podwójny pierwiastek) lub =2 lub x=−2
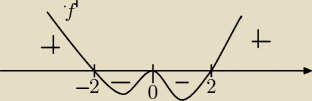
Badamy jak zachowuje się pochodna , kiedy dodatni, kiedy ujemna
x2(x−2)*(x+2)>0
w x=0 nie ma ekstremum, bo pochodna nie zmienia znaku przy przejściu przez ten punkt
Dla x<−2 f(x) rosnąca dla x∊(−2; 2) malejąca w x=−2 f(x) ma maksimum lokalne
fmaks=f(−2)=77
dla x>2 funkcja rrrrosnąca , f(x) ma minimum lokalne dla x=2
fmin=f(2)=−51
f '(x)=15x4−60x2
15x4−60x2=0
15x2(x2−4)=0
x=0 (podwójny pierwiastek) lub =2 lub x=−2
Badamy jak zachowuje się pochodna , kiedy dodatni, kiedy ujemna
x2(x−2)*(x+2)>0
w x=0 nie ma ekstremum, bo pochodna nie zmienia znaku przy przejściu przez ten punkt
Dla x<−2 f(x) rosnąca dla x∊(−2; 2) malejąca w x=−2 f(x) ma maksimum lokalne
fmaks=f(−2)=77
dla x>2 funkcja rrrrosnąca , f(x) ma minimum lokalne dla x=2
fmin=f(2)=−51
 dzięki za poprawienie
dzięki za poprawienie
