dzieki ewa: w trójkącie ABC o polu 50 dm² bok AB ma długość 20 dm. punkt p leży na boku AC i |CP|=¹₅ |AC|. punkt Q leży na boku BC i |CQ| =¹₅ |BC|. oblicz długość odcinka PQ i pole trójkąta CPQ.

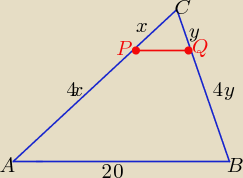
Eta: Trójkąty CPQi ABC są podobne

	|PC|		|CQ|		x		y		1
w skali k=		=		=		=		=		, x>0, y>0
	|AC|		|BC|		5x		4y		5

	1
to: |PQ|=		*|AB|=....
	5

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

P(CPQ)		1
	=		⇒ P(CPQ)=....
P(ABC)		25

Eta:

	y
Poprawiam chochlika : ....=
	5y

Pele: Git