f. jack: co to znaczy że funkcja osiąga wartość największą równą 12 dla argumentu 1?

Basia: To znaczy, że f(1)=12 (wartość funkcji dla x=1 jest równa 12) i dla każdego x∊D_f i x≠1 f(x)<12

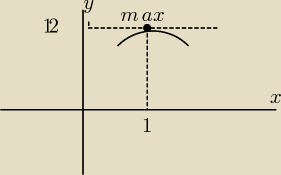
AS: Dokładam swoje trzy grosze. Oznacza to,że dla x = 1 przyjmuje wartość 12,największą z otoczenia x = 1 tzn, na lewo i prawo od x = 1 przyjmuje wartości mniejsze.od 12 (w pewnym zakresie) Punkt ten nazywamy maksimum lokalnym w przeciwieństwie do minimum.

Basia: Asie wartość największa to nie to samo co maksimum lokalne. Wartość najmniejsza to nie to samo co minimum lokalne. Na przykład funkcja f(x) =¹₃x³ − x ma maksimum lokalne dla x=−1 i minimum lokalne dla x=1 natomiast nie ma ani wartości najmniejszej, ani wartości największej bo przy x→−∞ f(x)→−∞ przy x→+∞ f(x)→+∞

AS: Nie doczytałaś dokładnie. Przecież w maksimum funkcja przyjmuje wartość największą w otoczeniu tego punktu. Ilustruje to rysunek. I o co chodzi?

Basia: Doczytałam. Wartość największą w pewnym otoczeniu dlatego nazywamy maksimum lokalnym, a nie wartością największą, że nazwa wartość największa została zarezerwowana dla faktycznej wartości największej w całej dziedzinie funkcji lub w zadanym z góry przedziale. To samo dotyczy minimum lokalnego i wartości najmniejszej. Funkcja może mieć dowolnie wiele maksimów lokalnych i jedną i tylko jedną wartość największą albo nie mieć jej wcale.