Prawdopodobieństwo warunkowe, a kombinatoryka V.Abel: Witam! Mam ogromną prośbę, czy zechciałby ktoś wyjaśnić jak liczyć prawdopodobieństwo warunkowe nie koniecznie za pomocą drzewka. Czyli jak to robić bardziej kombinatorycznie i proszę o pomoc w zadaniu: Na egzaminie należy wylosować 3 pytania z 10. Student umie odpowiedzieć na 7 pytań. Zda egzamin, jeśli odpowie na co najmniej 2 pytania. Oblicz prawdopodobieństwo, że zda, jeśli na pierwsze pytanie: a) umie odpowiedzieć b) nie umie odpowiedzieć. No więc ja mam : A− zda B− pod warunkiem, że umie na pierwsze ... pomocy

Mati_gg9225535: U U U U U U U N N N 1 2 3 4 5 6 7 8 9 10 ogolnie ze zbioru 10 pytan losujac 3 moze je wylosowac na (10 * 9 * 8) = 720 sposobów a) na pierwsze pytanie zna odp wiec moze je wylosowac na 7 sposobów, wiemy ze musi zdac wiec na drugie pytanie tez musi znac odpowiedz − na 6 sposobow moze wylosowa to pytanie (z siedmiu jedno juz wylosowal wczesniej) no i trzecie pytanie dowolnie z 10 pozostalo 8 wiec na tyle sposobow moze wylosowac trzecie pytanie. mamy więc: 7*6*8 = 336 sposobów

	336		7
P(A) =		=
	720		15

b) na pierwsze pytanie nie zna odpowiedzi, moze je wylosowac na 3 sposoby, zeby zdac na pozostale dwa musi znac odpowiedz wiec losuje drugie na 7 sposobow i trzecie na 6 sposobów − bo jedno juz wylosował tutaj mamy: 3*7*6 = 126

	126		7
P(B) =		=
	720		40

V.Abel: ok, ale odpowiedzi w książce to :

	11
a)
	12

	7
b)
	12

Mila: To jest prawdopodobieństwo warunkowe. Uwzględniając kolejność: Ω=10*9*8 A− wylosował pierwsze pytanie na które umie odpowiedzieć. B− zdał egzamin pod warunkiem, że na pierwsze wylosowane pytanie umiał odpowiedzieć P(B/A)=U{P(A∩B)}{P{A)} A: zdarzenia sprzyjające: (UUU),(UUN),(UNU)(UNN) |A|=7*6*5+7*6*3+7*3*6+7*3*2=504

	504		56		7
P(A)=		=		=
	10*9*8		80		10

A∩B: umiał odpowiedzieć na pierwsze pytanie i zdał egzamin |A∩B|=7*6*5+7*6*3+7*3*6=462

	462		231
P(A∩B)=		=
	10*9*8		10*9*4

	231		10		33		11
P(B/A)=		*		=		=
	10*36		7		36		12

Punkt zrób podobnie.

V.Abel: Ok, dzięki, wyszło, ale muszę przyznać, że pracochłonne 1. Mam pytanie − kiedy stosujemy metodę drzewek( do jakiego rodzaju prawdopodobieństwa), a kiedy kombinatorykę, żeby zadania liczyć optymalnie szybko ? . . 2. Podpowiesz jeszcze w tym zadaniu? : w urnach są kule białe i czarne; czarnych jest dwa razy więcej niż białych;wyciągamy dwie kule; oblicz dla jakiej liczby kul, prawdopodobieństwo, że wylosujemy dwie kule czarne wynosi

	2
		? ? ? ja to zrobiłem drzewem, ale najciekawsze w tym jest, to, że na gałęzich
	5

	2		1
czarna−czarna mam odpowiednio prawdopodobieństwa :		i		, brak zmiennych, czy to
	3		2

znaczy, że te prawdopodobieństwa nie zależą od ilości kul? Ratunku!. .

Mila: 1) nB,2nC n+2n=3n −liczba kul

	(3n) 2		1
Ω=		=		(3n)*(3n−1)
			2

A − wyciągnięto dwie kule czarne,

	(2n) 2		2n*(2n−1)
|A|=		=		=n(2n−1)
			2

	2
P(A)=
	5

	2*n(2n−1)
P(A)=		⇔
	3n(3n−1)

2*n(2n−1)		2
	=
3n(3n−1)		5

n=2 2 kule B 4 kule C 2) drzewko

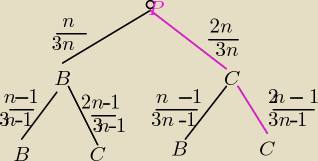
Mila: W tym zadaniu,lepij za pomocą drzewka, jeśli nie jesteś biegły we wzorach

	2		2n−1		2
P(CC)=		*		=
	3		3n−1		5

2(2n−1)		2
	=
3(3n−1)		5

V.Abel: Aaaaa Ale ja jestem na tej drugiej gałęzi odjąłem x zamiast 1 Mila jesteś nieoceniona jest jakaś reguła kiedy drzewo, kiedy wzór ? . .

Eta: drzewo w lecie ... w zimie kombinacje Tak sobie żartuję

Mila: Eta ma dobry humor, to miło, bo jakoś tak smutno ostatnio na forum i nie ma Ajtka i jego muzyki. Jeśli mało gałązek, to drzewko dobrze obrazuje niektóre procesy. Trzeba porozwiązywać trochę zadań, aby mieć wyczucie. Z jakiego zbioru zadań korzystasz?

PuRXUTM: Witam wszystkich Eta powaliło mnie to Te kombinacje to od kombinacji norweskich ?

V.Abel: Zbiór zadań, Podkowa. Podręcznik Nowa Era tylko to tak różnie, czasami wydaje się, że kombinatoryka, a potem słyszysz " drzewo" lub odwrotnie...

Mila: Rób zadania wszystkie po kolei, wątpliwości pisz, podawaj odpowiedzi, bo łatwo coś zgubic. Ważne jest , aby dobrze policzyć, drzewko to nic złego, chociaz nie wszyscy lubią ten sposób.

Trivial: Niektórzy wręcz nienawidzą.

V.Abel: w szkole stawiają na drzewa, są ok ale kombinatoryki nie chciałbym zaniedbać