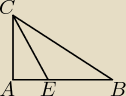
 Dany jest trójkąt prostokątny ABC, w którym ∡BAC=90 oraz |AC|=12. Na boku AB tego trójkąta
zaznaczono punkt E w taki sposób, że |CE|=|EB|. Wiedząc, że pole trójkąta ABC jest równe 108,
oblicz:
a) pole trójkąta BCE
b) wysokość trójkąta BCE poprowadzoną z punktu E.
Wszystkie jednostki podane są w cm.
Dany jest trójkąt prostokątny ABC, w którym ∡BAC=90 oraz |AC|=12. Na boku AB tego trójkąta
zaznaczono punkt E w taki sposób, że |CE|=|EB|. Wiedząc, że pole trójkąta ABC jest równe 108,
oblicz:
a) pole trójkąta BCE
b) wysokość trójkąta BCE poprowadzoną z punktu E.
Wszystkie jednostki podane są w cm.
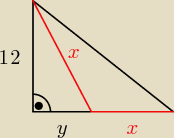
| 12*(y+x) | ||
PABC = | = 108 ⇒ x+y = 18 | |
| 2 |
 wiemy też, ze x ≥ 12
wiemy też, ze x ≥ 12