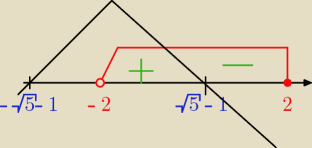
.. asdf: ekstrema:

	2x
x * √
	2+x

D: x ≠ −2

2−x
	≥ 0
2+x

(2−x)(2+x) ≥ 0 x ∊ <−2;2>, uwzgledniając dziedzine: x ∊(−2;2> teraz liczę pochodną:

	2x		2x
y' = x' * √		+ (√		)' * x =
	2+x		2+x

(...) =

	2−x		4x
√		−
	2+x		2−x   2√ * (2+x)2   2+x

i teraz przyrównuję do zera:

	2−x		4x
y' = 0, ⇒ √		−		= 0
	2+x		2−x   2√ * (2+x)2   2+x

do wspólnego mianownika:

2−x   2−x   √ *2√ *(2+x)2 − 4x   2+x   2+x
	= 0
2−x   2√ * (2+x)2   2+x

pierwiastki łączę:

2−x   2 * * (2+x)2 − 4x   2+x
	= 0
2−x   2√ * (2+x)2   2+x

	1
ucinam		z (2+x)2:
	2+x

2 *(2−x)(2+x) − 4x
	= 0
2−x   2√ * (2+x)2   2+x

2*(4 − x2) − 4x
	= 0
2−x   2√ * (2+x)2   2+x

8 − 2x2 − 4x
	= 0 // * mianownik:
2−x   2√ * (2+x)2   2+x

zniknęła czerwona dwójka: 4 − x² − 2x = 0 Δ = 20

	2 − 2√5
x1 =		= √5 − 1
	−2

x₂ = − √5 − 1 zaznaczam na osi przedziały, z prawej strony od dołu, wyszło mi: f(x) ↗ x ∊ (−2;√5−1) f(x) ↘ x ∊ (√5 − 1; 2> maksimum lokalne w punkcie: x = √5 − 1; f(√5 −1)

	2x
f(x) = x * √
	2+x

dobrze? i czy na końcu może być domknięta dwójka, czy nie? (chodzi o przedział domknięty)

asdf: funkcja wygląda tak:

	2 − x
x * √		, minus mi sie nie wbił na początku i przy liczeniu pochodnej (pochodną
	2+x

dobrze policzylem jak by co, tylko co z resztą..)

asdf: .

aniabb: w pochodnej na górze nie masz 4x a tylko samo 4

asdf: to jeszcze jest pomnożone * x, to jak?

aniabb: zrozumiałam że sam nawias liczysz

aniabb: domknięta dwójka ..dobrze

asdf: ok, dzieki