trójkąt olka: jak się za to zabrać? W trójkącie równoramiennym długość podstawy wynosi 16 cm, a długość wysokości poprowadzonej na tę podstawę jest równa 15 cm. oblicz długości pozostałych wysokości. chodzi tu o te zależności okręgu opisanego na trójkącie i wpisanego

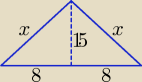
Bogdan: Wystarczy wzór Pitagorasa dla trójkątów prostokątnych dla wyznaczenia długości x ramienia,

	1		1
a następnie zastosowanie wzoru na pole trójkąta: P =		*16*15, P =		x*h,
	2		2

gdzie h to długość wysokości opuszczonej na ramię trójkąta równoramiennego.

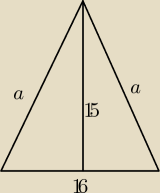
evil_woodworm: Zakładam, że jeżeli piszesz "podstawa" maż na myśli ten jeden bok inny od równych ramion. Wtedy Podana wysokosć dzieli podstawę na pół i można ładnie wyliczyć z tw.Pitagorasa pozostałe boki. Co do wysokości, to podpowiedź −skorzystaj z pola

evil_woodworm: Oj, Bogdan mnie uprzedził Ale przynajmniej upewniłam się, że zrobiłam dobre założenie co do podstawy

olka: wyszło mi,że ramie ma długość 17 cm PΔ=120 cm² czy aby obliczyć to szukane h trzeba wyliczyć je z : 120=17/2*h bo ja tak robie i mi dziwna liczba wychodzi:(

evil_woodworm: Owszem. Nie wychodzi ładnie niestety...

olka: ale tak ma być?

evil_woodworm: Na to wygląda

olka: to dobrze ulżyło mi..

evil_woodworm:

Zośka: Liczba to liczba, nie ma dziwnych liczb. Jedynie w epoce kamienia łupanego liczono posługując się początkowymi dodatnimi liczbami naturalnymi, mówiono wtedy np. tak: jedno drzewo, dwa drzewa, trzy drzewa, las. My już dawno wyrośliśmy z tej epoki, jesteśmy wykształceni (chyba) i znamy liczby wymierne, niewymierne i wiele innych, ale są to tylko liczby, nie ma potrzeby wpadać w popłoch widząc liczbę inną niż naturalna.

olka: masz rację Zośka, ale jak mi takie coś wychodzi to zaraz myślę, że raczej jest źle