wielomiany Anszej: dla jakich wartosci parametru a reszta z dzielenia wielomianu W(x)=2x⁴ − 3x³ +ax²+a²x + 2 prze dwumian x−1 jest wieksza od 3 proszę o rozwiazanie i wytlumaczenie krok po kroku

evil_woodworm: rozwiazuje...

evil_woodworm: 1.Dzielisz wielomian W(x) przez dwumian. (ja to zrobie schematem Hornera, ale mozesz to zrobić w "zwykły spoób" jak to masz wytłumaczone obok w dziale "wielomiany") 2 −3 a a² −2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 1 2 −1 a−1 a−1+a² a−1+a²−2 To na czerwono to jest nasza reszta, która wynosi a²+a−3 po zredukowaniu wyrazów podobnych (nie redukowałam na bieżąco).

evil_woodworm: 2.Musimy znalezć takie wartości a, dla których ta reszta będzie większa od 3, więc powstaje nam taka oto nierównosć kwadratowa: a²+a−3>3 3.Rozwiązuję nierównosć: a²+a>0 a(a+1)>0 a₁=−1 a₂=0

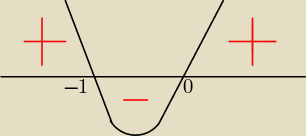
evil_woodworm: 4.Przedstawiam na osi

evil_woodworm: 5.Odzczytujemy wartości większe od 0, więc te z przedziałów znajdujących się nad osią. 6.Odp. a∊(−∞;−1)∪(0;∞)

evil_woodworm: Jakieś pytania?

Anszej: Dzięki za odpowiedź, wszystko jasne, w książce jest jednak odpowiedź (−∞, −2) (1,∞)

evil_woodworm: hmmm... pewnie zrobiłam gdzie jakiś błąd, którego nie widzę grunt, żebys zrozumiał metodę...

evil_woodworm: dobra, widzę + na − zamieniłam na samym poczatku−.−

evil_woodworm: tak, zgadza się, wtedy wychodzi nierówność a²+a+1>3 i po rozwiązaniu wychodzi tak jak w książce. Głupi błąd zrobiłam, sorry

Anszej: super, wieeeelkie dzięki!