Funkcja kwadratowa z parametrem Rafał: Wyznacz wszystkie całkowite wartości , dla których funkcja f(x)= ^k2−k−2_k−4x²−(k−2)x + k − 4 osiąga minimum i ma dwa różne miejsca zerowe.

Aga1.:

k2−k−2
	≠0
k−4

Δ>0

Rafał: Niestety Aga1 nie. a>0 ponieważ funkcja osiąga minimum. Ramiona paraboli idą do góry. Δ>0 wiem, ale właśnie w delcie mi wielomian 3 stopnia wychodzi i mam z tym problem,.

Rafał: Bo czuję,że Δ spierniczyłem tylko nie wiem w którym momencie.

Cusack: a miałeś w szkole dział wielomiany? Czy dopiero przy kwadratowej jesteś?

Aga1.: @ Rafał , masz rację, nie wiem dlaczego odczytałam,że funkcja ma ekstremum ( a nie minimum)

Rafał: Ja się do matury przygotowuje Rozwiązanie mam, tylko go nie rozumiem. Mianowicie Δ=(k−2)²−4(k²−k−2) Nie rozumiem za bardzo, bo podstawienie nie pasuje do wzoru na Δ. No i mianownik z k−4 gdzieś uciekł

Saizou :

	k2−k−2
Δ=(−(k−2))2−4*(k−4)*		=k2−4k+4−4k2+4k+8=−3k2+12>0
	k−4

−3k²>−12 k²<4 k<2 i k>−2 k∊(−2:2) jeśli się nie pomyliłem

Rafał: No to szczerze nie wiem czemu mi ten wielomian wychodzi.

Saizou :

k2−k−2
	>0
k−4

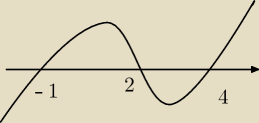
(k−4)(k²−k−2)>0 k²−k−2=0 k−4=0 Δ=1+8=9 k=4

	1−3
k1=		=−1
	2

	1+3
k2=		=2
	2

k∊(−1:2)u (4:+∞) ostatecznie k∊(−1:2)

Rafał: Tak, ten rozwiązałem. Łatwizna Tylko,że w Δ też mi wychodzi.