Wykaż że trójkąt ODE jest podobny do trójkąta ADE nat.: W trójkącie równobocznym ABC wysokości AE i CD przecinają się w punkcie O. a) Wykaż, że w trójkąt ODE jest podobny do tr. ADE. Oblicz skalę tego podobieństwa. b) Wiedząc dodatkowo, że obwód trójkąta ODE wynosi 2, oblicz długość boku trójkąta ABC. Wynik przedstaw w postaci a+b{c}, gdzie a,b,c należy do C i c>0

nat.: * tam gdzie jest {c} powinno być pierwiastek z c

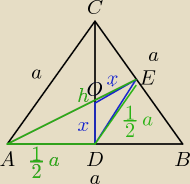
Beti: a)

	1		a√3		a√3
x = |OD| = |OE| =		*		=
	3		2		6

	a√3
h = |AE| =
	2

	|AD|		1   a 2		a		6		3
k1 =		=		=		*		=		= √3
	|OD|		a√3   6		2		a√3		√3

	|AE|		a√3   2		a√3		2
k2 =		=		=		*		= √3
	|DE|		1   a 2		2		a

czyli: k₁ = k₂ = √3 −−> trójkąty są podobne (cecha bbb), a skala podob. wynosi √3

Beti: b) obwód L_ODE = 2 więc:

1		a√3
	a + 2*		= 2 /*6
2		6

3a + 2√3a = 12 a(3+2√3) = 12

	12
a =
	3+2√3

dokończ, czyli usuń niewymierność z mianownika i zapisz w wymaganej postaci.

biedrona: to jest źle Beti, w a wyjdzie √3/3