obrotowe kici: Przekrój osiowy stożka jest trójkątem prostokątnym. Objętość stożka wynosi 216π. Oblicz pole powierzchni całkowitej tej bryły.

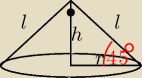
Beti: V = 216π πr²h = 216π/:π r²h = 216 i h = r (bo trójkąt o bokach h,r,l jest prostokątny równoramienny) r³ = 216 r = 6 h = 6

	r
cos45o =
	l

√2		6
	=
2		l

	12
l =		= 6√2
	√2

P_c = πr²+πrl podstaw dane i policz

kici: ale y stożka nie liczy sie jako 1/3PpH ?

Beti: O fakt Sorry

Tomasz: beti skąd wiesz że trójkąt prostokątny w tym zadaniu to trójkąt równoramienny

Beti: bo trójkąt złożony z tworzących i średnicy podstawy jest równoramienny, czyli kąty przy podstawie są równe, czyli mają po 45^o. Skoro kąty przy podstawie maja po 45^o, to trójkąt o bokach h,r,l ma kąty: 90^o, 45^o i trzeci musi mieć 45^o, czyli też jest równoramienny. Nie wiem, czy jasno to napisałam...

kici: ale jeśli zapiszę objętość ze wzoru to mi koszmarne liczby wychodzą! Nie da się ładnie wyliczyć promienia Nie wiem czy to dobrze czy jest błąd w treści.

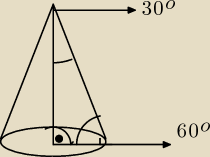
Tomasz: taki stożek według Ciebie nie ma prawa istnieć? czy czegoś nie rozumiem

MQ: @Tomasz Nie rozumiesz albo treści zadania albo pojęcia "przekrój osiowy stożka"

korek: V stożka jest równe chyba 1/3πr²h w tym zadaniu ktoś podał wzór objętości stożka πr²h