geomteria analltyczna sylw: sprawdź czy punkt P(6,1) leży na dwusiecznej kąta ABC trójkąta o wierzchołkach A(1,9) B(−3,1) C(2,−9)

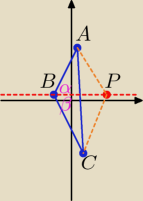
Bogdan: Jeśli punkt P(6, 1) leży na dwusiecznej kąta ABC, to α = β (oznaczenia wg rysunku). Można to zadanie rozwiązać na różne sposoby, m.in. następująco: Skorzystamy z twierdzenia cosinusów dla trójkąta ABP oraz dla trójkąta CBP. ΔABP:

	|AB|2 + |BP|2 − |AP|2
|AP|2 = |AB|2 + |BP|2 − 2|AB|*|BP|*cosα ⇒ cosα =
	2|AB|*|BP|

ΔCBP:

	|BC|2 + |BP|2 − |CP|2
|CP|2 = |BC|2 + |BP|2 − 2|BC|*|BP|*cosα ⇒ cosβ =
	2|BC|*|BP|

Teraz trzeba wyznaczyć długości odcinków: AB, BC, BP, AP, CP i wstawić otrzymane liczby do wzorów: cosα = ... , cosβ = ... , a następnie porównać wyniki. Po wykonaniu obliczeń otrzymamy odpowiedź: punkt P leży na dwusiecznej kąta ABC.

Eta: Podam jeszcze inny sposób rozwiazania zad. tw. jeżeli punkt należy do dwusiecznej kąta to dlległości tego punktu od ramion kąta są równe zatem wyznaczam równanie prostej AB

	yA −yb
pr.AB: y − yA=		*( x − xA) , bo xA≠xB
	xA − xB

po podstawieniu i przekształceniu otrzymasz: pr.AB: −2x +y −7=0 P(6,1) wyznaczamy odległość

	I−2*6 +1*1 −7I		18
d1=		=
	√5		√5

podobnie : pr.BC: 2x +y +5=0 ( policz i takie równanie prostej otrzymasz)

	2*6 +1*1 +5I		18
więc d2=		=
	√5		√5

wniosek : d₁= d₂ więc punkt P należy do dwusiecznej kąta ABC

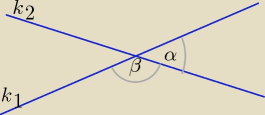Bogdan: Jeszcze inny sposób. Wykorzystamy wzór na tg kąta zawartego między prostymi: k₁: y = a₁x + b₁ k₂: y = a₂x + b₂

	|a1 − a2|
tgα =
	|1 + a1*a2|

Wartość bezwzględna daje tg kąta ostrego α, a nie tg kąta rozwartego β. Za chwilę podam to rozwiązanie.

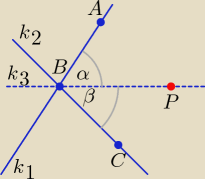Bogdan: A = (1, 9), B = (−3, 1), C = (2, −9), P = (6, 1), kąty α i β są ostre. Jeśli α = β, to prosta k₃ jest dwusieczną kąta ABC. Wyznaczamy współczynniki kierunkowe a₁, a₂, a₃ prostych: k₁, k₂, k₃.

	9 − 1		−9 − 1		1 − 1
a1 =		= 2, a2 =		= −2, a3 =		= 0
	1 + 3		2 + 3		6 + 3

	|a3 − a1|		|0 − 2|
tgα =		=		= 2
	|1 + a3*a1|		|1 + 0*2|

	|a3 − a2|		|0 + 2|
tgβ =		=		= 2
	|1 + a3*a2|		|1 + 0*(−2)|

tgα = tgβ to α = β, a więc prosta k₃ jest dwusieczną kąta ABC i punkt P leży na tej dwusiecznej.

Eta:

sylw: czy nie uważacie że to zadanie wykracza poza materiał maturalny? bo tego nie ma nawet w tablicach /

Eta: Witam sposób rozwiązania , który podałam z pewnością obejmuje materiał obowiazujacy w LO może tylko równania prostych wyznaczonych przez dwa punkty piszecie tak: y = ax +b ( warto zapamietać wzór , który podałam, bardzo upraszcza obliczenia, do wyznaczenia równania tej prostej. Pozdrawiam

sylw: to że jest w materiale lo to tak, ale nie musi być w materiale maturalnym, wiadomo jaki jest to okrojony test