.

. asdf: Witam, całki.. ∫ lnx dx, liczę przez części: u = ln v' = x dobrze?

20 lut 23:54

Dominik: ln = l * n

20 lut 23:54

Mila: Nie.

	1
[u=lnx ; du=		; dv=1stad v=∫1dx=x]
	x

20 lut 23:59

ICSP: https://matematykaszkolna.pl/strona/2294.html

21 lut 00:03

asdf:

Ekstremum lokalne: y = x* e^1/x D: x e (−∞;0)(0;∞)

	x*e^1/x
y' = x' * e^1/x + (e^1/x)'x = e^1/x + e^1/x x * (1/x)' = e^1/x −
	x²

D: x e(−∞;0)(0;∞) y' = 0

	x*e^1/x
e^1/x −		= 0
	x²

	x
e^1/x(1 −		) = 0 // : e^1/x
	x²

	1
(1 −		) = 0 // * x²
	x

x² − x = 0 x(x−1) = 0 x =0 ; x = 1 i teraz uwzględnia się x = 0 do przedziałów monotoniczności, ale w tym punkcie nie bedzie ekstremum?

21 lut 00:22

Roman: Nie

21 lut 00:38

asdf: a jak?

21 lut 00:43

Roman: No nie ma ekstremum w x=0

21 lut 00:46

asdf: no nie ma ekstremum − to napisałem, ale x=0 ma wpływ na monotoniczność..

21 lut 00:47

asdf: ?

21 lut 00:47

Mila:

	e^1/x
y'=e^1/x−
	x

f'(x) jest nieokreślona w x=0 f(x) jest nieokreślona w x=0 to o ekstremum nie może być mowy. Oblicz granice f(x)−obustronne w x=0 ( ciekawy problem) Jeśli chodzi o monotoniczność, badasz jak zachowuje się w dziedzinie pochodna− kiedy ujemna, kiedy dodatnia. Gdzies już rozwiązywałam to zadanie− przebieg zmienności tej funkcji.

21 lut 18:46

Mila: ?

21 lut 23:55

asdf: Zrobiłem tak: uwzględniłem x = 0 jako zmiana monotoniczności, a w tym punkcie, ze ekstremum nie istnieje. odpowiedź to: rośnie dla x e (−niesk.;−5)u(−1;niesk.) maleje dla x e (−5;−1) Dziękuję za pomoc.

22 lut 00:02

asdf: przepraszam, to nie do tego odpowiedź emotka

22 lut 00:03

asdf: f rosnie dla x e ( −niesk, 0)u(1;niesk) f maleje dla x e (0;1) minimum lokalne w pkt (1;e)

22 lut 00:05

Mila: Ponadto x=0 prawostronna asymptota pionowa y=x+1 asymptota ukośna

22 lut 00:34

Mila:

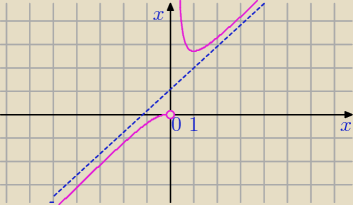
22 lut 00:35

asdf: Dziękuję Ci bardzo emotka

Całe badanie funkcji − to dopiero później emotka

22 lut 00:36