Rozwiąż graficznie nierówność. wajdzik: Rozwiąż graficznie nierówność:

	2x−3
|		|(całe w wartości bezwzględnej) <1
	x+1

D=R\{−1}

2x+1)−5		−5
	=		+2
x+1		x

W: [−1,2]

	2x−3
|		|(całe w wartości bezwzględnej) <1
	x+1

2x−3
	−1<0
x+1

2−3−x−1
	<0
x+1

x−4
	<0
x+1

(x−4)(x+1)<0 x=4 x=−1 Po narysowaniu wykresu, równania, przestawieniu i odwróceniu.. rozwiązaniem nierówności jest...? Naprawdę nie mam pojęcia. Myślę, że wszystko dobrze zrobiłem do tego momentu ale nie mam pojęcia jakie jest rozwiązanie. Mógłby ktoś pomóc? Z góry dziękuję za pomoc. Pozdrawiam

wajdzik: Mógłby ktoś mi pomóc?

wajdzik: Mógłby ktoś mi pomóc?

Beti:

	−5
po pierwsze wyrażenie zapisane w postaci kanonicznej ma postać:		+ 2
	x+1

po drugie rozwiązując nierówność musisz rozpatrzyc dwa przypadki:

	2x−3
|		| < 1
	x+1

↙ ↘

	2x−3		2x−3
		< 1 i		> −1
	x+1		x+1

wajdzik: A więc mamy: 1. x=4 x=−4 <0

	2
2. x=		x=−1 >0
	3

Biorąc pod uwagę mój wykres to coś na pewno się zgadza. Tylko nie widzi mi się, że tam jest

	2
to		. Ogólnie nie mam pojęcia jakie jest rozwiązanie.
	3

Przypuszczam, że takie: 1. x∊(−∞,−1) U (4,+∞)

	2
2. x∊(−1,		)
	3

A rozwiązaniem tej nierówności będzie:

	2
x∊ (−∞,		) U (4,+∞)
	3

Czy dobrze myślę?

wajdzik: ?

wajdzik: Czy mógłby ktoś pomóc?

MQ: Jeśli masz rozwiązać to graficznie, to:

	2x−3
1. Rysujesz y=
	x+1

2. To co masz pod osią OX, odbijasz symetrycznie wzgl. osi OX 3. Rysujesz kreskę y=1 4. Zaznaczasz na osi OX te wartości x, dla których wykres leży pod kreską.

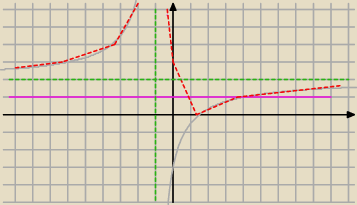
Aga1.: Graficznie rysujesz wykres

	2x−3
y=I		I −−kolor czerwony i y=1 −−różowy
	x+1

I patrzysz dla jakich x czerwony wykres jest pod różową prostą. (zielone to asymptoty)

wajdzik: Tak jest, wszystko mam dokładnie tak narysowane. Czyli rozwiązaniem nierówności jest: x∊(−1,4) ?

MQ:

	2
Wg mnie (		,4)
	3