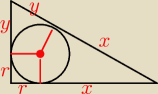
Zadanie sience fiction Basia: Spotkałam się z takim oto zadaniem (arkusze przygotowujące do matury − podstawa) Dany jest trójkąt prostokątny o obwodzie 20 opisany na okręgu o promieniu r=2. Znajdź promień R okręgu opisanego na tym trójkącie. Jest oczywiste, że 2x+2y+2r=20 2x+2y+4=20 2x+2y=16 x+y=8

	x+y
R=		=4
	2

i taka też jest odpowiedź, chociaż sposób rozwiązania podany przez autorów bardzo skomplikowany nie wiadomo po co. Rzecz w tym, że albo taki trójkąt nie istnieje, albo gdzieś popełniam idiotyczny błąd. (to już nie należy do rozwiązania, ale....................) (x+2)²+(y+2)²=(x+y)² (x+2)²+(8−x+2)²=8² (x+2)²+(10−x)²=8² x²+4x+4+100−20x+x²=64 2x²−16x+104−64=0 2x²−16x+40=0 x²−8x+20=0 Δ=64−4*20=64−80=−16 < 0 czyli równanie nie ma rozwiązania czyli taki trójkąt nie istnieje. Czy takie zadanie "sience fiction" powinno w ogóle istnieć ?

Bogdan: W trójkącie prostokątnym o przyprostokątnych długości: a, b i przeciwprostokątnej długości c, średnica okręgu wpisanego ma długość: 2r = a + b − c, promień okręgu opisanego ma

	c
długość R =		,
	2

r − długość promienia okręgu wpisanego w ten trójkąt. Obwód trójkąta L = a + b + c. Mamy dwie równości: a + b + c = 20 i a + b − c = 4, które odejmujemy stronami otrzymując:

	c
2c = 16 ⇒ R =		= 4
	2

Basia: Bogdanie tyle to ja wiem. Przeczytaj co napisałam dalej !

Bogdan: Podałem inny sposób rozwiązania tego zadania, ale masz rację Basiu, taki trójkąt nie istnieje. Można to sprawdzić również tak: Jeśli a + b + c = 20 i c = 8 to a + b = 12, stąd b = 12 − a Na podstawie tw. Pitagorasa: a² + b² = c² ⇒ a² + (12 − a)² = 64. Stąd: 2a² − 24a + 80 = 0 ⇒ a² − 12a + 40 = 0, Δ = 144 − 160 < 0

Basia: No całe szczęście. Już myślałam, że kompletnie zgłupiałam. A jak zareaguje uczeń, jeżeli nieopatrznie przyjdzie mu do głowy policzyć sobie długości boków tego trójkąta "sienece fiction" ?

Eta: np: dla Ob = 24 a nie 20 wówczas R= 5 , i trójkąt istnieje a= 8 b= 6 c= 10 Może chodziło o to ,by wykazać ,że taki trójkąt nie istnieje.

Bogdan: Trudno uwierzyć, że w zadaniu maturalnym (na poziomie podstawowym) wystąpiłby taki problem. Myślę, że błędny zapis dotyczący obwodu powstał podczas druku.

Basia: Nie sądzę. Autorzy w rozwiązaniu (bardzo skomplikowanym) doprowadzili wynik do postaci R=4 i na tym poprzestali. To tylko mnie się zachciało policzyć boki tego trójkąta (nie wiadomo po co, bo zadanie tego nie wymagało). No i efekt jaki jest każdy widzi. Tak sobie napisałam z nadzieją, że jakiś autor może przeczyta i zastanowi się w przyszłości nad zadaniami, które "podrzuca" młodzieży do rozwiązywania. Bo wydaje mi się, że jednak takie gafy nie powinny się zdarzać.

Basia: Niemożliwe Bogdanie. Zamieszczono rozwiązanie. Długie jest. Nie chce mi się przepisywać. Drukarz musiałby całe rozwiązanie dostosować do swojej pomyłki.

Eta: Basiu tylko czy autor tego zad. przeczyta to co napisałaś .

Bogdan: W takim razie nie jest to gafa, to bubel i wstyd dla autora.

Eta: W ciągu ostatnich 45 minut na forum pojawili się: AROB, Bogdan, Basia, Eta oraz 3 gości My czekamy na zadania a młodzież się bawi

Eta: Dobranoc! Miłych snów

Bogdan: Dobranoc

Basia: Znalazłam ten arkusz w sieci. Oto link: http://bi.gazeta.pl/im/0/5751/m5751380.pdf Kolorowych snów.

Basia: Przeczyta mam nadzieję. Jutro skopiuję to wszystko i wyślę do GW. Ewentualnie poszukam kontaktu z autorką. Podpisała się. Anna Zalewska.

Bogdan: Anna Zalewska jest znaną autorką podręczników i zbiorów zadań z matematyki, w tym maturalnych zbiorów zadań.

Bogdan: Dobry wieczór Basiu. Napisałaś do GW?

Basia: Napisałam, z prośbą o przekazanie listu pani Zalewskiej. Sądzę wprawdzie, że ona już dawno wie, że to zadanie nie było w porządku, ale przede wszystkim chodziło mi o podkreślenie faktu, że zupełnie niepotrzebnie skomplikowała rozwiązanie naprawdę prostego zadanka.