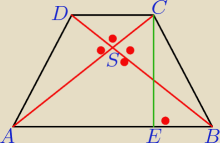
 czerwone kropki to kąty proste
ponieważ trapez jest równoramienny to
|AS|=|BS|=x
|CS|=|DS|=y
oblicz x i y z tw.Pitagorasa
mając x i y także z tw.Pitagorasa oblicz |BC|
czerwone kropki to kąty proste
ponieważ trapez jest równoramienny to
|AS|=|BS|=x
|CS|=|DS|=y
oblicz x i y z tw.Pitagorasa
mając x i y także z tw.Pitagorasa oblicz |BC|
| |AB|−|CD| | 20−12 | |||
|EB| = | = | =4 | ||
| 2 | 2 |
 dobra "dusza" , ta Nasza Basia
dobra "dusza" , ta Nasza Basia 
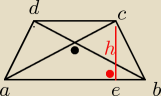 JA BYM TU SKORZYSTAŁA Z TWIERDZENIA PITAGORASA...
EB=20−12=8/2=4 CM
AE=20−4=16 CM
ALE NIE WIEM SKĄD WZIĄĆ DŁUGOŚĆ PRZEKĄTNEJ
JA BYM TU SKORZYSTAŁA Z TWIERDZENIA PITAGORASA...
EB=20−12=8/2=4 CM
AE=20−4=16 CM
ALE NIE WIEM SKĄD WZIĄĆ DŁUGOŚĆ PRZEKĄTNEJ ?
?
 Olka nadal nie wie jak policzyć długość przekątnej mimo mojej podpowiedzi.
To teraz Ty się pomęcz.
Ja nie wiem co jeszcze można podpowiedzieć nie rozwiązując po prostu zadania od początku
do końca
Olka nadal nie wie jak policzyć długość przekątnej mimo mojej podpowiedzi.
To teraz Ty się pomęcz.
Ja nie wiem co jeszcze można podpowiedzieć nie rozwiązując po prostu zadania od początku
do końca
 . DZIĘKUJE BASIU
. DZIĘKUJE BASIU

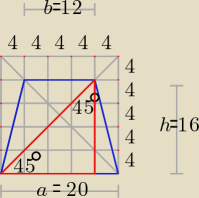 Jeśli wykonamy taki rysunek, to zobaczymy wskazówki i wszystkie dane liczbowe potrzebne do
obliczenia pola powierzchni tego trapezu.
Jeśli wykonamy taki rysunek, to zobaczymy wskazówki i wszystkie dane liczbowe potrzebne do
obliczenia pola powierzchni tego trapezu.

 Witam wszystkich
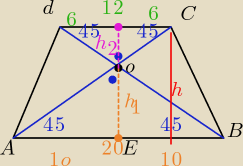
Witam wszystkich podam rozwiaząnie tak:
h= h1 + h2
twierdzenie: długość wysokości trójkąta poprowadzonej
z wierzchołka kąta prostego jest średnią geometryczną długości odcinków
na jakie dzieli ona przeciwprostokatną
( myslę ,że właśnie o to twierdzenie chodziło w pytaniu zadania.
stąd:
h12 = 6*6 => h1= 6
h22= 10*10 => h2 = 10
zatem h= 16
podobnie mozna :
trójkaty są prostokątne i równoramienne
więc IABI −−− długość przekatnej kwadratu
to h1= 12IABI = 10
h2 = 12IDCI= 6
czyli h(trap.) = 16
podam rozwiaząnie tak:
h= h1 + h2
twierdzenie: długość wysokości trójkąta poprowadzonej
z wierzchołka kąta prostego jest średnią geometryczną długości odcinków
na jakie dzieli ona przeciwprostokatną
( myslę ,że właśnie o to twierdzenie chodziło w pytaniu zadania.
stąd:
h12 = 6*6 => h1= 6
h22= 10*10 => h2 = 10
zatem h= 16
podobnie mozna :
trójkaty są prostokątne i równoramienne
więc IABI −−− długość przekatnej kwadratu
to h1= 12IABI = 10
h2 = 12IDCI= 6
czyli h(trap.) = 16















 Eta − Mark − łobuzica
Eta − Mark − łobuzica 














 ten "typ" tak ma
ten "typ" tak ma