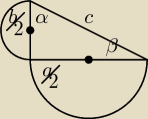
trójkąt prostokątny pepe: Na bokach trójkąta prostokątnego zakreślono półkola o średnicach równych długości danego boku. Wiedząc ,że suma pól tych półkoli jest 10razy większa od pola tego trójkata, wyznaczyć wartość tgα +tgβ, gdzie α, β są kątami ostrymi tego trójkąta.

Basia: P₁ = π(^a₂)² P₂ = π(^b₂)² P_T = ^a*b₂ P₁+P₂ = 10*P_T ^π₄*(a²+b²) = 5ab a²+b² = ^20ab_π tgα+tgβ=^a_b+^b_a = ^a2+b2_ab=

20abπ		20ab		20
	=		=
ab		πab		π

pepe: Diękuję bardzo

Basia: Zrozumiałeś wszystko ? Jeśli nie to pytaj.

pepe: tak, rozumiem

pepe: Mam jeszcze takie zadanie: W rozwartokątnym trójkącie równoramiennym ABC, IACI=IBCI odległość środka koła wpisanego w trójkąt od wierzchołka A ma długość d. Kąt rozwarty ma miarę 2α. Wyznaczyć pole tego trójkąta i długość promienia R okręgu opisanego na tym trójkącie. rozwiaząłem to zad. tak: ( nie wiem czy dobrze? , bo nie mam odp) Sporządziłem rys. oznaczyłem: IABI=a ICDI= h kąt ACB= 2α IAOI= d kątCAD= 90^o − α i kąt DAO = 45^o − ^α₂ bo AO jest dwusieczną kąta CAD policzyłem z trójkąta prostokatnego ADO że a= 2d*cos( 45^o −^α₂) oraz z trójkąta ADC h= ^a₂*ctgα podstawiłem za a i otrzymałem h= d*ctgα*cos( 45^o − ^α₂) pole wyszło mi P= d²*cos²(45^o −^α₂)*ctgα promień R policzyłem ze wzoru sinusów

	2d*cos(45o −α2)
wyszło mi R=
	sin2α

czy to wszystko? i czy dobrze liczyłem? Bardzo proszę o sprawdzenie

Basia: Wszystko o.k. Brawo!

pepe: Ufff, dziękuję i życzę miłego dnia

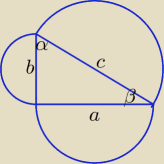
Bogdan: Witaj Basiu. Myślę, że w rozwiązaniu zadania o półkolach trzeba wprowadzić sprostowania. W zadaniu jest informacja mówiąca, że półkola zbudowano na bokach trójkąta prostokątnego, a nie na przyprostokątnych tego trójkąta. Ponadto w zadaniu jest mowa o półkolach, a nie o kołach.

	1		a
P1 =		π(		)2
	2		2

	1		b
P2 =		π(		)2
	2		2

	1		c
P3 =		π(		)2
	2		2

	1
c2 = a2 + b2, PΔ =		ab
	2

P₁ + P₂ + P₃ = 10P_Δ

Basia: Witaj Bogdanie! Oczywiście masz rację. Jakoś niedokładnie przeczytałam to zadanie.

Bogdan: No to dokończmy.

1		a2		1		b2		1		c2		1
	π*		+		π*		+		π*		= 10 *		ab
2		4		2		4		2		4		2

1		8
	π(a2 + b2 + c2) = 5ab / *		i c2 = a2 + b2
8		π

	40		40		1
a2 + b2 + a2 + b2 =		ab ⇒ 2(a2 + b2) =		ab / *
	π		π		2ab

a2 + b2		20
	=
ab		π

a		b		20
	+		=
b		a		π

	20
tgα + tgβ =
	π

Basia: Co najśmieszniejsze wynik jest identyczny. Z przyczyn oczywistych. P₃ = P₁+P₂

Bogdan: No właśnie. Warto tu zauważyć, że twierdzenie Pitagorasa w postaci: jeśli trójkąt jest prostokątny,to suma pól kwadratów zbudowanych na przyprostokątnych jest równa polu kwadratu zbudowanego na przeciwprostokątnej przyzwyczaiło nas do kwadratów, a przecież to twierdzenie zachowuje prawdziwość nie tylko dla kwadratów, ale także dla figur podobnych zbudowanych na bokach trójkąta prostokątnego, mogą to być np. półkola, trójkąty równoboczne, pięciokąty równoboczne, itd.

pepe: Rozwiązywałem podobnie,

	πd2
Pk=		, d − średnica okręgu
	4

	πa2
P1(półkola)=
	8

	πb2
P2=
	8

	πc2
P3=
	8

P₁ +P₂+P₃= 10*P_Δ ^π₈(a²+b²+c²)=5*ab , a²+b²= c^{2 π}₈*2c²= 5ab /*4

	c2
πc2= 20ab i tgα+tgβ=
	ab

	20
podstawiłem do równania i otrzymałem tgα+tgβ=
	π

taki sam wynik jak u Basi i Bogdana dziękuję za wyjasnienia